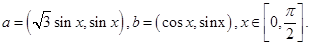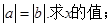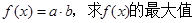题目内容
已知向量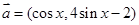 ,
,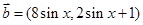 ,
, ,设函数
,设函数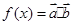 .
.
(1)求函数 的最大值;
的最大值;
(2)在 中,角
中,角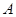 为锐角,角
为锐角,角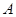 、
、 、
、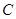 的对边分别为
的对边分别为 、
、 、
、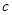 ,
,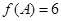 ,且
,且 的面积为3,
的面积为3,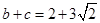 ,求
,求 的值.
的值.
(1) ;(2)
;(2) .
.
解析试题分析:(1)利用向量的数量积,二倍角公式,辅助角公式把 化为
化为
 的形式,再确定最大值;(2)根据三角形的面积公式,余弦定理求解.
的形式,再确定最大值;(2)根据三角形的面积公式,余弦定理求解.
试题解析:(1)

∴ . (6分)
. (6分)
(2)由(1)可得 ,∴
,∴ ,
,
因为 ,所以
,所以 ,
, ,∴
,∴ , (8分)
, (8分)
∵ ,∴
,∴ ,又
,又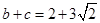 , (10分)
, (10分)
∴
 ,
,
∴ . (12分)
. (12分)
考点:向量的数量积,二倍角公式,辅助角公式,余弦定理.

练习册系列答案
相关题目
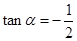 ,求
,求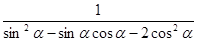 的值;
的值;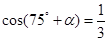 ,且
,且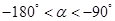 ,求
,求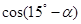 的值.
的值.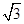 sinωxcosωx(ω>0)的最小正周期为π,
sinωxcosωx(ω>0)的最小正周期为π,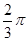 ]上的值域.
]上的值域.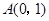 ,
,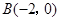 ,
,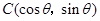 (
(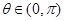 ),
),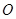 为坐标原点,向量
为坐标原点,向量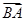 与向量
与向量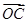 共线.
共线.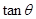 的值;
的值;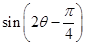 的值.
的值.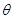 的直线
的直线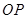 与单位圆在第一象限的部分交于点
与单位圆在第一象限的部分交于点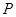 ,单位圆与坐标轴交于点
,单位圆与坐标轴交于点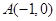 ,点
,点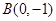 ,
, 与
与 轴交于点
轴交于点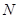 ,
, 与
与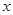 轴交于点
轴交于点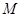 ,设
,设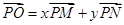
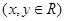
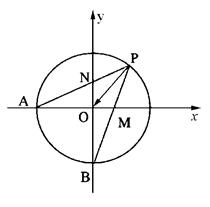
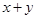 的最小值.
的最小值.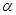 为第三象限角,
为第三象限角,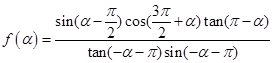 .
.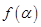 (2)若
(2)若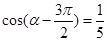 ,求
,求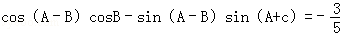 .
.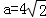 ,b=5,求向量
,b=5,求向量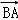 在
在 方向上的投影.
方向上的投影. ),其中ω>0,|
),其中ω>0,|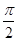 ,若cos
,若cos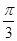 cos
cos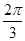 sin
sin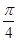 .
.