题目内容
(2012•道里区三模)已知P为边长为2的正方形ABCD及其内部一动点,若△PAB,△PBC面积均不大于1,则
•
取值范围是( )
| AP |
| BP |
分析:设点P(x,y),由已知条件可得x,y满足的可行域,利用数量积可得要求的问题,进而即可解决.
解答:解:如右图所示: 设点P(x,y).
设点P(x,y).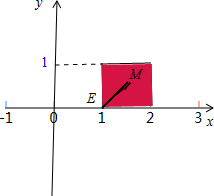
∵△PAB,△PBC面积均不大于1,
∴
×2y≤1,
×2(2-x)≤1,0≤x≤2,0≤y≤2.
解得0≤y≤1,1≤x≤2.如左图所示的可行域:
由
•
=(x,y)•(x-2,y)=x(x-2)+y2=(x-1)2+y2-1.
∵d2=(x-1)2+y2表示的是可行域中的任意一点M与E(1,0)的距离的平方,
∴0≤d2≤(
)2,∴-1≤d2-1≤1,即-1≤
•
≤1.
故选D.
 设点P(x,y).
设点P(x,y).
∵△PAB,△PBC面积均不大于1,
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得0≤y≤1,1≤x≤2.如左图所示的可行域:
由
| AP |
| BP |
∵d2=(x-1)2+y2表示的是可行域中的任意一点M与E(1,0)的距离的平方,
∴0≤d2≤(
| 2 |
| AP |
| BP |
故选D.
点评:利用面积和向量的数量积正确得出x,y的取值范围及要解决的问题和充分结合图形是解题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
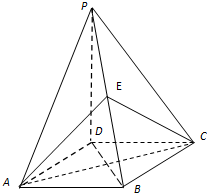 (2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
(2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上. (2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=
(2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=