题目内容
设 =(2cos
=(2cos ,1),
,1), =(cos
=(cos ,
, sin2
sin2 ),
), =
= ·
· ,
,
 R.
R.
⑴若 =0且
=0且
 [
[ ,
, ],求
],求 的值;
的值;
⑵若函数 =
= (
( )与
)与 的最小正周期相同,且
的最小正周期相同,且 的图象过点(
的图象过点( ,2),求函数
,2),求函数 的值域及单调递增区间.
的值域及单调递增区间.
(1) ;(2)
;(2) 的值域为
的值域为 ,单调递增区间为
,单调递增区间为 .
.
解析试题分析:(1)首先利用平面向量的坐标运算及和差倍半的三角函数公式,
将 化简为
化简为 =
= ,
,
根据 =0及
=0及
 [
[ ,
, ]求解.
]求解.
(2)首先确定得到 =
= ,根据
,根据 ,得到
,得到 的值域为
的值域为 ,
,
单调递增区间为 .
.
试题解析:(1) =
= ·
· =
=

 =
= 3分
3分
由 得
得 =0
=0
∴ ∵
∵
 [
[ ,
, ]∴
]∴ ∴
∴
∴ 6分
6分
(2)由(1)知 ∴
∴
 ∴
∴ 8分
8分
∴ =
=

∴ 的值域为
的值域为 ,单调递增区间为
,单调递增区间为 . 12分
. 12分
考点:平面向量的坐标运算,三角函数的和差倍半公式,三角函数的性质.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
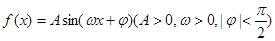 的图象的一部分如下图所示.
的图象的一部分如下图所示.
 的解析式;
的解析式; 时,求函数
时,求函数 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值. 函数
函数 .
. 的最小正周期及单调递减区间;
的最小正周期及单调递减区间; 的对边分别是
的对边分别是 ,且满足
,且满足 求
求 的取值范围.
的取值范围. .
. 的最小正周期;
的最小正周期; 时,求实数
时,求实数 的值,使函数
的值,使函数 并求此时
并求此时 上的对称中心.
上的对称中心. ,
, ,且
,且

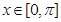 的单调增区间;
的单调增区间; 为何值,直线
为何值,直线 与函数
与函数 )(ω>0,0<
)(ω>0,0<
 =
= ,且a∈(0,
,且a∈(0,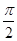 ),求f(a)的值.
),求f(a)的值. ,
, ,其中
,其中 ,若函数
,若函数 ,且函数
,且函数 的图象与直线y=2两相邻公共点间的距离为
的图象与直线y=2两相邻公共点间的距离为 .
. 的值;
的值; ,求△ABC周长的取值范围.
,求△ABC周长的取值范围.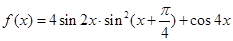 .
. 的最小正周期;
的最小正周期; 在
在 处取得最大值,求
处取得最大值,求 的值;
的值; 的单调递增区间.
的单调递增区间.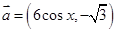 ,
,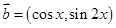 ,
,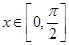 .(1)若
.(1)若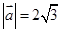 ,求
,求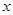 的值;
的值;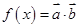 ,求
,求 的最大、最小值.
的最大、最小值.