题目内容
[2012·四川卷] 如图1-3,半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作与平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,该交线上的一点P满足∠BOP=60°,则A、P两点间的球面距离为( )
A.Rarccos![]() B.
B.![]()
C.Rarccos![]() D.
D.![]()
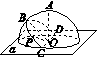
图1-3
A [解析] 由已知,OA⊥CD,又B点到平面α的距离最大,即B点在半圆CBD的最高点,即半圆弧CBD的中点,于是BO⊥CD,于是CD⊥平面AOB,进而平面CBD⊥平面AOB,
且∠AOB为二面角A-CD-B的平面角,该角等于平面BCD与α所成二面角的余角,为45°,
于是由公式cos∠AOP=cos∠AOBcos∠BOP=![]() ·
·![]() =
=![]() ,即∠AOP=arccos
,即∠AOP=arccos![]() ,
,
故A、P两点间的球面距离为Rarccos![]() .
.

练习册系列答案
相关题目


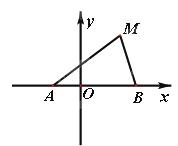 (2012年高考四川卷理科21) (本小题满分12分) 如图,动点
(2012年高考四川卷理科21) (本小题满分12分) 如图,动点