题目内容
在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域,点E正北55海里处有一个雷达观测站A。某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40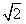 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+θ(其中sinθ=
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+θ(其中sinθ=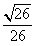 ,0°<θ<90°)且与点A相距10
,0°<θ<90°)且与点A相距10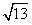 海里的位置C。
海里的位置C。
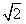 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+θ(其中sinθ=
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+θ(其中sinθ=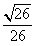 ,0°<θ<90°)且与点A相距10
,0°<θ<90°)且与点A相距10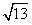 海里的位置C。
海里的位置C。
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由。
(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由。
解:(1)如图,AB=40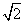 ,AC=10 ,AC=10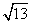 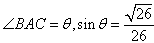 由于 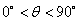 所以cosθ= 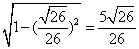 由余弦定理得BC= 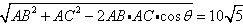 所以船的行驶速度为 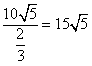 (海里/小时); (海里/小时); |
|
| (2)如图所示,以A为原点建立平面直角坐标系,设点B、C的坐标分别是B(x1,y2),C(x1,y2),BC与x轴的交点为D 由题设有x1=y1= 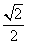 AB=40 AB=40x2=ACcos 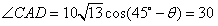 y2=ACsin 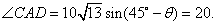 所以过点B、C的直线l的斜率k= 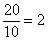 直线l的方程为y=2x-40 又点E(0,-55)到直线l的距离d= 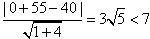 所以船会进入警戒水域。 |
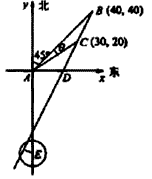 |

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
 在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40
在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40 在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域,点E正北方向55海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40
在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域,点E正北方向55海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40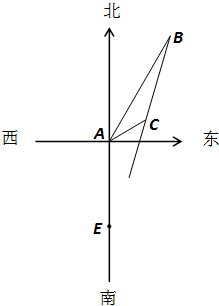 如图所示,在一个特定时段内,以点E为中心的10海里以内海域被设为警戒水域.点E正北40
如图所示,在一个特定时段内,以点E为中心的10海里以内海域被设为警戒水域.点E正北40 海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20
海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20 且与点A相距40
且与点A相距40 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东 (其中sin
(其中sin ,
, )且与点A相距10
)且与点A相距10 海里的位置C.
海里的位置C.