Question

证明不等式(n∈N^*)

Answer 1

证明略

解析:

证法一: (1)当n等于1时，不等式左端等于1，右端等于2，所以不等式成立:

(2)假设n=k(k≥1)时，不等式成立，即1+＜2，

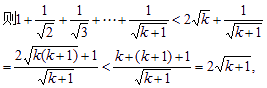
∴当n=k+1时，不等式成立.

综合(1)、(2)得:当n∈N^*时，都有1+＜2.

另从k到k+1时的证明还有下列证法:

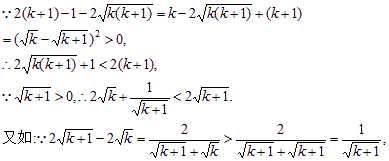
证法二: 对任意k∈N^*，都有:

  

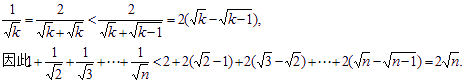
证法三:设f(n)= 

那么对任意k∈N^* 都有:

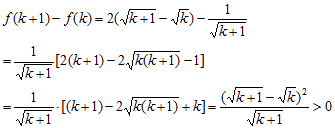
∴f(k+1)＞f(k)

因此，对任意n∈N^* 都有f(n)＞f(n－1)＞…＞f(1)=1＞0，

∴