题目内容
若x＞0，y＞0，x+2y=1，（1）求xy的最大值．
（2）求
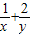的最小值．
【答案】分析：（1）由基本不等式可得，xy=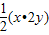
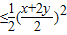可求
（2）由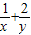
=（
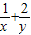）（x+2y）=5
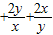可求
解答：解：（1）∵x＞0，y＞0，x+2y=1，
∴xy=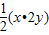
=
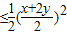即xy的最大值为
，
（2）∵
=（
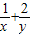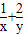）（x+2y）=5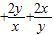
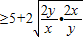=9
当且仅当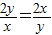
即x=y=
时取等号
∴
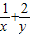的最小值为9．
点评：本题主要考查了利用基本不等式求解最值，解题的关键是公式的灵活应用及基本不等式应用条件的配凑
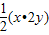
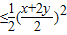可求（2）由
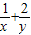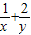=（）（x+2y）=5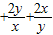可求解答：解：（1）∵x＞0，y＞0，x+2y=1，
∴xy=
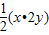
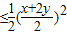=即xy的最大值为
，（2）∵
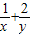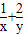=（）（x+2y）=5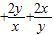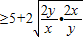=9当且仅当
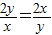即x=y=时取等号∴
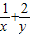的最小值为9．点评：本题主要考查了利用基本不等式求解最值，解题的关键是公式的灵活应用及基本不等式应用条件的配凑
练习册系列答案
相关题目
A（不等式选做题）若x＞0，y＞0且x+2y=1，则