题目内容
(本小题满分13分)已知函数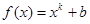 (其中
(其中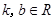 且
且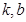 为常数)的图像经过点A
为常数)的图像经过点A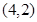 、B
、B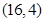 .
.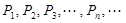 是函数
是函数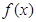 图像上的点,
图像上的点,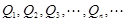 是
是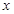 正半轴上的点.
正半轴上的点.
(1) 求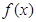 的解析式;
的解析式;
(2) 设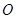 为坐标原点,
为坐标原点,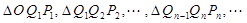 是一系列正三角形,记它们的边长是
是一系列正三角形,记它们的边长是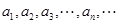 ,求数列
,求数列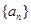 的通项公式;
的通项公式;
(3) 在(2)的条件下,数列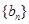 满足
满足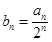 ,记
,记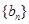 的前
的前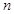 项和为
项和为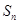 ,证明:
,证明: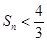 。
。
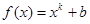 (其中
(其中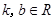 且
且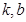 为常数)的图像经过点A
为常数)的图像经过点A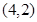 、B
、B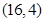 .
.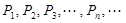 是函数
是函数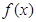 图像上的点,
图像上的点,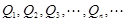 是
是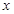 正半轴上的点.
正半轴上的点.(1) 求
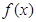 的解析式;
的解析式;(2) 设
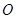 为坐标原点,
为坐标原点,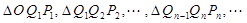 是一系列正三角形,记它们的边长是
是一系列正三角形,记它们的边长是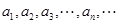 ,求数列
,求数列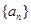 的通项公式;
的通项公式;(3) 在(2)的条件下,数列
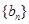 满足
满足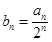 ,记
,记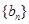 的前
的前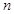 项和为
项和为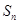 ,证明:
,证明: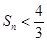 。
。(1) ;(2)
;(2) ;(3)
;(3) ,所以
,所以
 .,两式相减得:
.,两式相减得: ,整理得:
,整理得: .
.
 ;(2)
;(2) ;(3)
;(3) ,所以
,所以 .,两式相减得:
.,两式相减得: ,整理得:
,整理得: .
.试题分析:(1)


 .
.(2)由
 .
.由

将
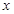 代人
代人 ,由此原问题转化为:
,由此原问题转化为:“已知
 且
且 ,求
,求 ”.
”.又
 ,两式相减可得:
,两式相减可得:



又,因为
 ,所以
,所以 ,
, 从而
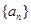 是以
是以 为首项,
为首项, 为公差的等差数列,即
为公差的等差数列,即 .
. (3)
 ,所以
,所以 .
.两式相减得:

整理得:
 .
.点评:错位相减法是一种常用的数列求和方法,应用于等比数列与等差数列相乘的形式。 形如An=BnCn,其中Bn为等差数列,Cn为等比数列;分别列出Sn,再把所有式子同时乘以等比数列的公比,即qSn;然后错一位,两式相减即可。

练习册系列答案
相关题目
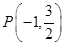 是椭圆E:
是椭圆E: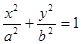 (
(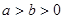 )上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
)上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.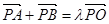 (
(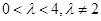 ).求证:直线AB的斜率为定值;
).求证:直线AB的斜率为定值;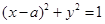 与双曲线
与双曲线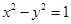 的渐近线相切,则
的渐近线相切,则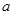 的值是 _______.
的值是 _______. 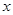 轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线
轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线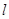 在
在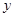 轴上的截距为
轴上的截距为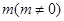 ,
,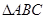 为直角三角形,三边长分别为
为直角三角形,三边长分别为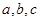 ,其中斜边AB=
,其中斜边AB=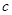 ,若点
,若点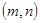 在直线
在直线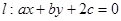 上运动,则
上运动,则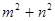 的最小值为
的最小值为 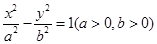 的一条渐近线经过点
的一条渐近线经过点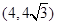 ,则该双曲线的离心率为___________.
,则该双曲线的离心率为___________. 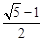 的椭圆称为“优美椭圆”.设
的椭圆称为“优美椭圆”.设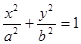
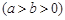 为“优美椭圆”,F、A分别是左焦点和右顶点,B是短轴的一个端点,则
为“优美椭圆”,F、A分别是左焦点和右顶点,B是短轴的一个端点,则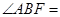 ( )
( )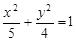 的右焦点
的右焦点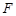 重合,过点
重合,过点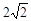 的直线与抛物线交于
的直线与抛物线交于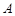 ,
,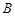 两点.
两点.
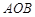 的面积.
的面积.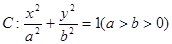 的离心率为
的离心率为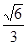 ,
,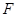 为椭圆的右焦点,
为椭圆的右焦点,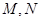 两点在椭圆
两点在椭圆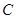 上,且
上,且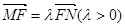 ,定点
,定点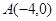 。
。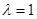 时,有
时,有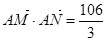 ,求椭圆
,求椭圆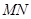 斜率为k,且设
斜率为k,且设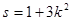 时,试求
时,试求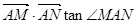 关于S的函数表达式f(s)的最大值,以及此时
关于S的函数表达式f(s)的最大值,以及此时