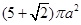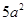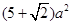题目内容
已知三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2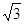 ,AB=1,AC=2,∠BAC=60°,则球O的表面积为
,AB=1,AC=2,∠BAC=60°,则球O的表面积为
A.4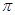 | B.12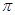 | C.16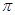 | D.64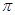 |
C
解析试题分析:由三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA="2" 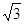 ,AB=1,AC=2,∠BAC=60°,知BC=
,AB=1,AC=2,∠BAC=60°,知BC=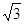 ,∠ABC=90°.故△ABC截球O所得的圆O′的半径r=
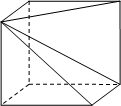
,∠ABC=90°.故△ABC截球O所得的圆O′的半径r= AC=1,由此能求出球O的半径,从而能求出球O的表面积。解:如图,
AC=1,由此能求出球O的半径,从而能求出球O的表面积。解:如图,
三棱锥S-ABC的所有顶点都在球O的球面上,∵SA⊥平面ABC,SA=2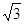 ,AB=1,AC=2,∠BAC=60°,∴BC=
,AB=1,AC=2,∠BAC=60°,∴BC=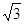 ,∴∠ABC=90°.∴△ABC截球O所得的圆O′的半径r=
,∴∠ABC=90°.∴△ABC截球O所得的圆O′的半径r= AC=1,∴球O的半径R=
AC=1,∴球O的半径R=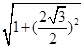 =2,∴球O的表面积S=4πR2=16π.故选C.
=2,∴球O的表面积S=4πR2=16π.故选C.
考点:球的表面积
点评:本题考查球的表面积的求法,合理地作出图形,数形结合求出球半径,是解题时要关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
三棱锥的三组相对的棱分别相等,且长度各为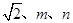 ,其中
,其中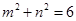 ,则该三棱锥体积的最大值为
,则该三棱锥体积的最大值为
A.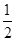 | B.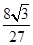 | C.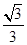 | D.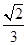 |
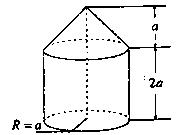
如图是某简单组合体的三视图,则该组合体的体积为( ) 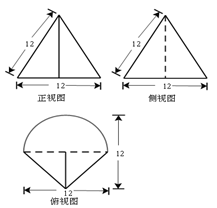
A.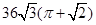 | B.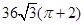 |
C.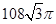 | D.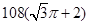 |

 , AC=2,若四面体ABCD体积的最大值为
, AC=2,若四面体ABCD体积的最大值为 ,则这个球的表面积为
,则这个球的表面积为 B.
B. C.
C. D.
D.
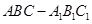 的主视图(又称正视图)是边长为4的正方形, 则此正三棱柱的侧视图(又称左视图)的面积为( )
的主视图(又称正视图)是边长为4的正方形, 则此正三棱柱的侧视图(又称左视图)的面积为( )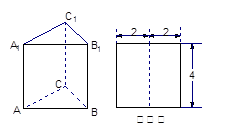
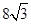


 ,则正视图与侧视图中x的值为( )
,则正视图与侧视图中x的值为( )
 .
.
 .
.
 .
.
 .
.