题目内容
14.已知$f(x)=\left\{\begin{array}{l}{2^x},x≤0\\{x^{\frac{1}{3}}},x>0\end{array}\right.$,若f(α)=1,则f(f(α-1))=( )| A. | $\frac{{\root{3}{4}}}{2}$或1 | B. | $\frac{1}{2}$或1 | C. | $\frac{1}{2}$ | D. | 1 |
分析 由f(α)=1可求得2α=1或${α}^{\frac{1}{3}}$=1,从而分类讨论求得f(f(α-1))的值.
解答 解:∵f(α)=1,
∴2α=1或${α}^{\frac{1}{3}}$=1,
∴α=0或α=1;
当α=0时,f(α-1)=2-1=$\frac{1}{2}$,
f(f(α-1))=f($\frac{1}{2}$)=$\frac{\root{3}{4}}{2}$;
当α=1时,f(α-1)=20=1,
f(f(α-1))=f(1)=1;
故选A.
点评 本题考查了分段函数的应用及复合函数的应用,同时考查了分类讨论的思想应用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
2.若函数$f(x)=\left\{\begin{array}{l}2x+2,x≤0\\{2^x}-4,x>0\end{array}\right.$,则f(f(1))的值为( )
| A. | -10 | B. | 10 | C. | -2 | D. | 2 |
9.集合A={x|x2-2x-8≤0},B={x|2x<8},则A∩B=( )
| A. | (-∞,2] | B. | [-2,3) | C. | [-4,3) | D. | (-∞,3] |
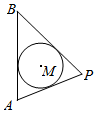 某建筑工地在施工过程中,为了保护一口直径为1米的圆形古井M,决定将其围起来,工地上现有一块长为2米(宽为1.2米)的木工板AB可利用,现将其围成高1.2米的围挡,如图,圆M与AB,PA,PB(PA,PB为另外两侧的围挡)均相切.
某建筑工地在施工过程中,为了保护一口直径为1米的圆形古井M,决定将其围起来,工地上现有一块长为2米(宽为1.2米)的木工板AB可利用,现将其围成高1.2米的围挡,如图,圆M与AB,PA,PB(PA,PB为另外两侧的围挡)均相切.