题目内容
函数f(x)=
的定义域为
| ||
| log2(x+2) |
(-2,-1)∪(-1,3]
(-2,-1)∪(-1,3]
.分析:由函数的意义可得
,从而可求得f(x)=
的定义域.
|
| ||
| log2(x+2) |
解答:解:依题意得:
,即
,
∴-2<x<-1或-1<x≤3.
故答案为:(-2,-1)∪(-1,3].
|
|
∴-2<x<-1或-1<x≤3.
故答案为:(-2,-1)∪(-1,3].
点评:本题考查函数的定义域及其求法,根据题意得到不等式组
并熟练解此不等式组是关键,易错点在于忽视分母为0的情况,属于中档题.
|

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
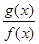 |≤
|≤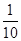 ,则称f (x)可被g(x)置换,那么下列给出的函数中能置换f (x)=
,则称f (x)可被g(x)置换,那么下列给出的函数中能置换f (x)=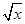 x∈[4,16]的是 ( )
x∈[4,16]的是 ( )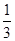 (x+8) x∈[4,16] D.g(x)=
(x+8) x∈[4,16] D.g(x)=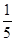 (x+6) x∈[4,16]
(x+6) x∈[4,16]