题目内容
设对任意实数x∈[-1,1],不等式x2+ax-3a<0恒成立,则实数a的取值范围是
- A.a>0
- B.

- C.a>0或a<-12
- D.
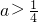
B
分析:法一:y=x2+ax-3a的对称轴是x= .①当-
.①当- ≥1时,x=-1时有最大值a>
≥1时,x=-1时有最大值a> ,与a≤-2相矛盾.②当
,与a≤-2相矛盾.②当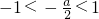 时,x=-1或x=1时,有最大值.x=-1有最大值a>
时,x=-1或x=1时,有最大值.x=-1有最大值a> ,故
,故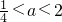 ;当x=1有最大值1-2a<0,a
;当x=1有最大值1-2a<0,a ,故
,故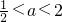 .③当
.③当 ≤-1,即a≥2时,x=1时有最大值1-2a<0,a
≤-1,即a≥2时,x=1时有最大值1-2a<0,a ,a≥2.由此能求出实数a的范围.
,a≥2.由此能求出实数a的范围.
法二:设f(x)=x2+ax-3a,由对任意实数x∈[-1,1],不等式x2+ax-3a<0恒成立,知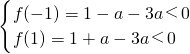 ,由此能求出实数a的范围.
,由此能求出实数a的范围.
解答:解法一:y=x2+ax-3a的对称轴是x= .
.
①当- ≥1,即a≤-2时,x=-1离对称轴最远,而函数开口向上,所以有最大值,
≥1,即a≤-2时,x=-1离对称轴最远,而函数开口向上,所以有最大值,
其最大值是a> ,与a≤-2相矛盾.
,与a≤-2相矛盾.
∴a∈∅;
②当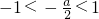 ,即-2<a<2时,
,即-2<a<2时,
x=-1或x=1时,有最大值.
由①知,x=-1有最大值时,其最大值是a> ,故
,故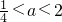 ;
;
当x=1有最大值时,其最大值是1-2a<0,即a ,故
,故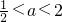 .
.
∴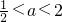 ;
;
③当 ≤-1,即a≥2时,
≤-1,即a≥2时,
x=1时有最大值,
其最大值是1-2a<0,a ,
,
∴a≥2.
综上所述,a> .
.
故选B.
解法二:设f(x)=x2+ax-3a,
∵对任意实数x∈[-1,1],不等式x2+ax-3a<0恒成立,
∴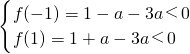 ,
,
即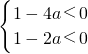 ,
,
∴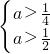 ,故
,故 .
.
故选B.
点评:本题考查函数的恒成立问题,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意分类讲座思想的合理运用.
分析:法一:y=x2+ax-3a的对称轴是x=
 .①当-
.①当- ≥1时,x=-1时有最大值a>
≥1时,x=-1时有最大值a> ,与a≤-2相矛盾.②当
,与a≤-2相矛盾.②当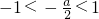 时,x=-1或x=1时,有最大值.x=-1有最大值a>
时,x=-1或x=1时,有最大值.x=-1有最大值a> ,故
,故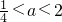 ;当x=1有最大值1-2a<0,a
;当x=1有最大值1-2a<0,a ,故
,故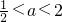 .③当
.③当 ≤-1,即a≥2时,x=1时有最大值1-2a<0,a
≤-1,即a≥2时,x=1时有最大值1-2a<0,a ,a≥2.由此能求出实数a的范围.
,a≥2.由此能求出实数a的范围.法二:设f(x)=x2+ax-3a,由对任意实数x∈[-1,1],不等式x2+ax-3a<0恒成立,知
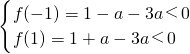 ,由此能求出实数a的范围.
,由此能求出实数a的范围.解答:解法一:y=x2+ax-3a的对称轴是x=
 .
.①当-
 ≥1,即a≤-2时,x=-1离对称轴最远,而函数开口向上,所以有最大值,
≥1,即a≤-2时,x=-1离对称轴最远,而函数开口向上,所以有最大值,其最大值是a>
 ,与a≤-2相矛盾.
,与a≤-2相矛盾.∴a∈∅;
②当
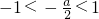 ,即-2<a<2时,
,即-2<a<2时,x=-1或x=1时,有最大值.
由①知,x=-1有最大值时,其最大值是a>
 ,故
,故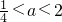 ;
;当x=1有最大值时,其最大值是1-2a<0,即a
 ,故
,故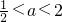 .
.∴
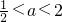 ;
;③当
 ≤-1,即a≥2时,
≤-1,即a≥2时,x=1时有最大值,
其最大值是1-2a<0,a
 ,
,∴a≥2.
综上所述,a>
 .
.故选B.
解法二:设f(x)=x2+ax-3a,
∵对任意实数x∈[-1,1],不等式x2+ax-3a<0恒成立,
∴
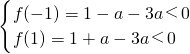 ,
,即
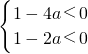 ,
,∴
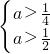 ,故
,故 .
.故选B.
点评:本题考查函数的恒成立问题,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意分类讲座思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目