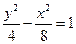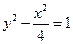题目内容
已知 为平面内两定点,过该平面内动点
为平面内两定点,过该平面内动点 作直线
作直线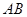 的垂线,垂足为
的垂线,垂足为 .若
.若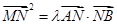 ,其中
,其中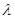 为常数,则动点
为常数,则动点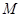 的轨迹不可能是( )
的轨迹不可能是( )
| A.圆 | B.椭圆 | C.抛物线 | D.双曲线 |
C
解析试题分析:不妨设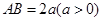 ,以
,以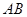 所在直线建立
所在直线建立 轴,以
轴,以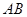 的中垂线所在直线建立
的中垂线所在直线建立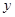 轴,则有
轴,则有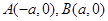 ,设
,设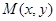 ,则
,则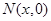 ,所以
,所以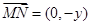 ,
,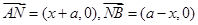
由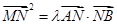 可得
可得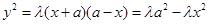 ,当
,当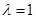 时,
时,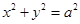 表示圆心在原点,半径为
表示圆心在原点,半径为 的圆;当
的圆;当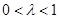 时,
时,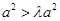 ,方程可化为
,方程可化为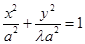 ,表示焦点在
,表示焦点在 轴上的椭圆;当
轴上的椭圆;当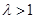 时,
时,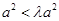 ,方程可化为
,方程可化为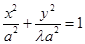 ,表示焦点
,表示焦点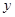 轴上的椭圆;当
轴上的椭圆;当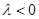 时,方程可化为
时,方程可化为 ,表示焦点在
,表示焦点在 轴的双曲线;当
轴的双曲线;当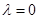 时,方程可化为
时,方程可化为 ,表示一条直线即
,表示一条直线即 轴;综上可知,动点
轴;综上可知,动点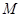 的轨迹不可能是抛物线,选C.
的轨迹不可能是抛物线,选C.
考点:曲线的轨迹问题.

练习册系列答案
相关题目
对于曲线 ∶
∶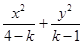 =1,给出下面四个命题:
=1,给出下面四个命题:
(1)曲线 不可能表示椭圆;
不可能表示椭圆;
(2)若曲线 表示焦点在x轴上的椭圆,则1<
表示焦点在x轴上的椭圆,则1<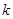 <
<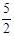 ;
;
(3)若曲线 表示双曲线,则
表示双曲线,则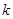 <1或
<1或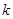 >4;
>4;
(4)当1<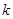 <4时曲线
<4时曲线 表示椭圆,其中正确的是 ( )
表示椭圆,其中正确的是 ( )
| A.(2)(3) | B.(1)(3) | C.(2)(4) | D.(3)(4) |
抛物线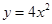 的焦点到准线的距离是( )
的焦点到准线的距离是( )
| A.2 | B.4 | C.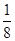 | D.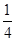 |
抛物线 的焦点到双曲线
的焦点到双曲线 的渐近线的距离是( )
的渐近线的距离是( )
A. |
B.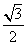 |
| C.1 |
D.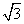 |
如图,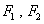 分别是双曲线C:
分别是双曲线C: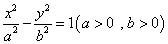 的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交与点M,若|MF2|=|F1F2|,则C的离心率是( )
的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交与点M,若|MF2|=|F1F2|,则C的离心率是( )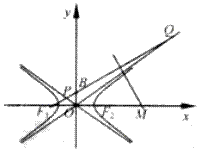
A.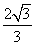 |
B.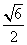 |
C. |
D.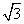 |
已知抛物线C: 的焦点为F,直线y=2x-4与C交于A,B两点.则cos∠AFB=( )
的焦点为F,直线y=2x-4与C交于A,B两点.则cos∠AFB=( )
A. |
B.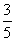 |
C.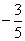 |
D. |
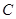 :
: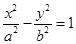
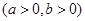 的焦距为
的焦距为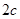 ,焦点到双曲线
,焦点到双曲线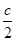 ,则双曲线
,则双曲线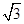
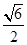
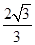
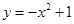 的顶点为A,与x 轴正半轴的交点为B,设抛物线与两坐标轴正半轴围成的区域为M,随机往M内投一点P, 则点P落在
的顶点为A,与x 轴正半轴的交点为B,设抛物线与两坐标轴正半轴围成的区域为M,随机往M内投一点P, 则点P落在 AOB内的概率是( )
AOB内的概率是( )
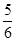
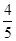
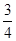
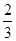
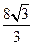 的双曲线方程为( )
的双曲线方程为( )