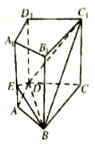
题目内容
【题目】已知圆![]() 关于直线
关于直线![]() 对称,圆心
对称,圆心![]() 在第二象限,半径为
在第二象限,半径为![]() .
.
(Ⅰ)求圆![]() 的方程.
的方程.
(Ⅱ)是否存在直线![]() 与圆
与圆![]() 相切,且在
相切,且在![]() 轴、
轴、![]() 轴上的截距相等?若存在,写出满足条件的直线条数(不要求过程);若不存在,说明理由.
轴上的截距相等?若存在,写出满足条件的直线条数(不要求过程);若不存在,说明理由.
【答案】(1) ![]() ;(2) 3条.
;(2) 3条.
【解析】试题分析:(1)根据圆心和半径写出圆C的标准方程;(2) 在![]() 轴、
轴、![]() 轴上的截距相等且不为
轴上的截距相等且不为![]() 时,设存在直线
时,设存在直线![]() 与圆
与圆![]() 相切; 在
相切; 在![]() 轴、
轴、![]() 轴上的截距相等且不为
轴上的截距相等且不为![]() 时,设存在直线
时,设存在直线![]() 与圆
与圆![]() 相切,,圆心到直线的距离为半径,求出参数的值,带回直线方程即可.
相切,,圆心到直线的距离为半径,求出参数的值,带回直线方程即可.
试题解析:
(Ⅰ)由题意知:圆心![]() ,半径
,半径![]() ,圆
,圆![]() .
.
(Ⅱ)在![]() 轴、
轴、![]() 轴上的截距相等且不为
轴上的截距相等且不为![]() 时,设存在直线
时,设存在直线![]() 与圆
与圆![]() 相切,
相切,
则圆心到直线的距离为半径![]() ,
,
所以![]() ,
,![]() 或
或![]() ,
,
直线方程为![]() ,
,![]() .
.
在![]() 轴、
轴、![]() 轴上的截距相等且不为
轴上的截距相等且不为![]() 时,设存在直线
时,设存在直线![]() 与圆
与圆![]() 相切,
相切,
则有![]() ,
,
所以,![]() ,
,
即:![]() ,综上知,存在直线
,综上知,存在直线![]() 与圆
与圆![]() 相切,且在
相切,且在![]() 轴、
轴、![]() 轴上的截距相等,
轴上的截距相等,
直线方程为![]() ,
,![]() ,
,![]() .
.

练习册系列答案
相关题目