题目内容
设a>1,则双曲线
-
=1的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| (a+1)2 |
A、(
| ||||
B、(
| ||||
| C、(2,5) | ||||
D、(2,
|
分析:根据题设条件可知:e2=(
)2=
=1+(1+
)2,然后由实数a的取值范围可以求出离心率e的取值范围.
| c |
| a |
| a2+(a+1)2 |
| a2 |
| 1 |
| a |
解答:解:e2=(
)2=
=1+(1+
)2,
因为
是减函数,所以当a>1时0<
<1,
所以2<e2<5,即
<e<
,
故选B.
| c |
| a |
| a2+(a+1)2 |
| a2 |
| 1 |
| a |
因为
| 1 |
| a |
| 1 |
| a |
所以2<e2<5,即
| 2 |
| 5 |
故选B.
点评:本题的高考考点是解析几何与函数的交汇点,解题时要注意双曲线性质的灵活运用.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
设k>1,则关于x,y的方程(1-k)x2+y2=k2-1所表示的曲线是( )
| A、长轴在x轴上的椭圆 | B、实轴在y轴上的双曲线 | C、实轴在x轴上的双曲线 | D、长轴在y轴上的椭圆 |
 的最大值为
的最大值为 ;②椭圆
;②椭圆 与椭圆
与椭圆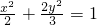 有相同的离心率;③双曲线
有相同的离心率;③双曲线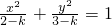 的焦点坐标是(1,0),(-1,0)④圆x2+y2=1与直线y=kx+2没有 公共点的充要条件是
的焦点坐标是(1,0),(-1,0)④圆x2+y2=1与直线y=kx+2没有 公共点的充要条件是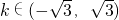 ⑤设a>1,则双曲线
⑤设a>1,则双曲线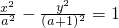 的离心率e的取值范围是
的离心率e的取值范围是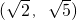 .
.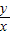 的最大值为
的最大值为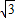 ;②椭圆
;②椭圆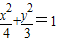 与椭圆
与椭圆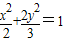 有相同的离心率;③双曲线
有相同的离心率;③双曲线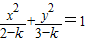 的焦点坐标是(1,0),(-1,0)④圆x2+y2=1与直线y=kx+2没有 公共点的充要条件是
的焦点坐标是(1,0),(-1,0)④圆x2+y2=1与直线y=kx+2没有 公共点的充要条件是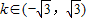 ⑤设a>1,则双曲线
⑤设a>1,则双曲线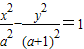 的离心率e的取值范围是
的离心率e的取值范围是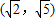 .
.