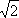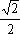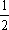题目内容
设向量 =(cos25°,sin25°),
=(cos25°,sin25°), =(sin20°,cos20°),若t为实数,且
=(sin20°,cos20°),若t为实数,且 ,则
,则 的最小值为 .
的最小值为 .
【答案】分析:求出  =( cos25°+tsin20°,sin25°+tcos20°),化简
=( cos25°+tsin20°,sin25°+tcos20°),化简 的解析式为
的解析式为 ,由二次函数的性质求得它的最小值.
,由二次函数的性质求得它的最小值.
解答:解:∵向量 =(cos25°,sin25°),
=(cos25°,sin25°), =(sin20°,cos20°),若t为实数,且
=(sin20°,cos20°),若t为实数,且 ,
,
∴ =( cos25°+tsin20°,sin25°+tcos20°).
=( cos25°+tsin20°,sin25°+tcos20°).
∴ =
= =
= =
= ≥
≥ ,
,
当且仅当t=- 时,等号成立,
时,等号成立,
∴ 的最小值为
的最小值为  ,
,
故答案为 .
.
点评:本题主要考查两个向量坐标形式的运算,向量的模的定义和求法,三角函数的恒等变换,化简 的解析式为
的解析式为 ,是解题的关键.
,是解题的关键.
 =( cos25°+tsin20°,sin25°+tcos20°),化简
=( cos25°+tsin20°,sin25°+tcos20°),化简 的解析式为
的解析式为 ,由二次函数的性质求得它的最小值.
,由二次函数的性质求得它的最小值.解答:解:∵向量
 =(cos25°,sin25°),
=(cos25°,sin25°), =(sin20°,cos20°),若t为实数,且
=(sin20°,cos20°),若t为实数,且 ,
,∴
 =( cos25°+tsin20°,sin25°+tcos20°).
=( cos25°+tsin20°,sin25°+tcos20°).∴
 =
= =
= =
= ≥
≥ ,
,当且仅当t=-
 时,等号成立,
时,等号成立,∴
 的最小值为
的最小值为  ,
,故答案为
 .
.点评:本题主要考查两个向量坐标形式的运算,向量的模的定义和求法,三角函数的恒等变换,化简
 的解析式为
的解析式为 ,是解题的关键.
,是解题的关键. 
练习册系列答案
相关题目
设向量
=(cos25°,sin25°),
=(cos25°,sin155°,则
•
的值为( )
| a |
| b |
| a |
| b |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|