题目内容
(本题满分14分)如图所示,圆柱的高为2,底面半径为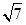 ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过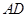 作圆柱的截面交下底面于
作圆柱的截面交下底面于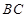 .
.
(1)求证: ;
;
(2)若四边形ABCD是正方形,求证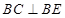 ;
;
(3)在(2)的条件下,求四棱锥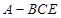 的体积.
的体积.

【答案】
(1)证明:在圆柱中:
 上底面//下底面,
上底面//下底面,
且上底面∩截面ABCD= ,下底面∩截面ABCD=
,下底面∩截面ABCD=
 //
//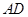 ……………………………………………………………………….2分
……………………………………………………………………….2分
又 AE、DF是圆柱的两条母线,
AE、DF是圆柱的两条母线,
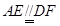
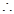
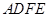 是平行四边形,所以
是平行四边形,所以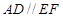 ,又
,又 //
//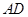
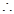
 …………………………………………………………………….5分
…………………………………………………………………….5分
(2)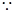 AE是圆柱的母线,
AE是圆柱的母线,
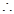
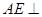 下底面,又
下底面,又
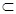 下底面,
下底面,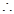
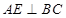 …………………………….7分
…………………………….7分
又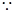 截面ABCD是正方形,所以
截面ABCD是正方形,所以 ⊥
⊥ ,又
,又
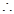
 ⊥面
⊥面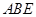 ,又
,又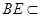 面
面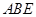 ,
,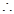
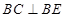 ……………………………9分
……………………………9分
(3)因为母线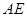 垂直于底面,所以
垂直于底面,所以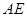 是三棱锥
是三棱锥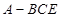 的高……………………10分,
的高……………………10分,
EO就是四棱锥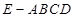 的高……………………10分
的高……………………10分
设正方形ABCD的边长为x,则AB=EF=x,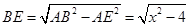
又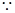
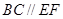 ,且
,且 ,
,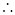 EF⊥BE,
EF⊥BE, 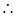 BF为直径,即BF=
BF为直径,即BF=
在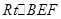 中,
中,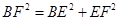
即
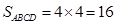 ,……………………………………………………………12分
,……………………………………………………………12分
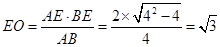
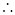
 ………………………14分
………………………14分
【解析】略

练习册系列答案
相关题目


 、
、 的边长都是1,平面
的边长都是1,平面 平面
平面 在
在 上移动,点
上移动,点 在
在 上移动,若
上移动,若 (
( )
)
 的长;
的长; 为何值时,
为何值时, 与面
与面 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小. ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC; 平面C1CBB1;
平面C1CBB1;