题目内容

对任意的实数a，关于x的方程log2［2x2+(m+3)x+2m］=a总有实数根.则m的取值范围为（    ）

A.［９，＋∞］                              B.（－∞，１）

C.（－∞，１）∪［９，＋∞)          D.以上都不正确

C

解析:由已知得函数f(x)=log2［2x2+(m+3)x+2m］的值域为R，即函数g(x)=2x2+(m+3)x+2m取任意的正数，故Δ=(m+3)2-4×2×2m≥0，解得m≤1或m≥9.

练习册系列答案
相关题目
已知f（x）是R上的单调函数，且对任意的实数a∈R，有f（-a）+f（a）=0恒成立，若f（-3）=2
（Ⅰ）试判断f（x）在R上的单调性，并说明理由；
（Ⅱ）解关于x的不等式：f(
m-xx
)+f(m)＜0，其中m∈R且m＞0．
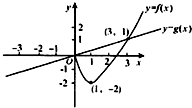精英家教网对任意的实数a，b，记max{a，b}=
a(a≥b)
b(a＜b)
若F（x）=max{f（x），g（x）}（x∈R），其中奇函数y=f（x）在x=1时有极小值-2，y=g（x）是正比例函数，函数y=f（x）（x≥0）与函数y=g（x）的图象如图所示  则下列关于函数y=F（x）的说法中，正确的是（　　）
A、y=F（x）为奇函数
B、y=F（x）有极大值F（1）且有极小值F（-1）
C、y=F（x）的最小值为-2且最大值为2
D、y=F（x）在（-3，0）上不是单调函数
对任意的实数a、b，记max{a，b}=
a(a≥b)
b(a＜b)
．若F（x）=max{f（x），g（x）}（x∈R），其中奇函数y=f（x）在x=l时有极小值-2，y=g（x）是正比例函数，函数y=f（x）（x≥0）与函数y=g（x）的图象如图所示．则下列关于函数y=F（x）的说法中，正确的是（　　）
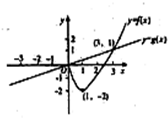（2011•烟台一模）对任意的实数a，b，记max{a，b}=
a(a≥b)
b(a＜b)
，若F（x）=max{f（x），g（x）}（x∈R），其中奇函数y=f（x）在x=1时有极小值-2，y=g（x）是正比例函数，函数y=f（x）（x≥0）与函数y=g（x）的图象如图所示，则下列关于函数y=F（x）的说法中，正确的是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网