题目内容
已知等比数列 的前
的前 项和为
项和为 ,正数数列
,正数数列 的首项为
的首项为 ,
,
且满足: .记数列
.记数列 前
前 项和为
项和为 .
.
(Ⅰ)求 的值; (Ⅱ)求数列
的值; (Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)是否存在正整数 ,且
,且 ,使得
,使得 成等比数列?若存在,求出
成等比数列?若存在,求出 的值,若不存在,说明理由.
的值,若不存在,说明理由.
【答案】
(Ⅰ)
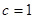 (Ⅱ)
(Ⅱ) 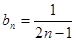
 (Ⅲ) 存在,
(Ⅲ) 存在, 。
。
【解析】熟练掌握并灵活运用等差等比数列的通项公式以及求和公式是解决此题的关键.
(Ⅰ)根据Sn求出a1,a2,a3,根据{an}为等比数列,确定出c的值.
(Ⅱ)根据bn+1=
|
bn |
|
1+2bn |
(n∈N*),得到bn与bn+1的递推关系,根据特殊的数列求通项.
(Ⅲ)先求出Tn,假设满足T1,Tm,Tn成等比数列,得到n与m的关系式,再根据1<m<n,求出m,n的范围,根据m,n是正整数,求出m,n的值.
解:(Ⅰ)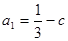 ,
, ,
, ………(3分)
………(3分)
因为 为等比数列所以
为等比数列所以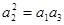 ,得
,得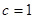 ………………………(4分)
………………………(4分)
经检验此时 为等比数列. ………………(5分)
为等比数列. ………………(5分)
(Ⅱ)∵ 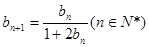 ∴
∴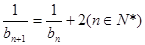
数列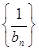 为等差数列 …………………………………………(7分)
为等差数列 …………………………………………(7分)
又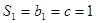 ,所以
,所以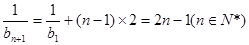
所以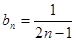
 …………(10分)
…………(10分)
(Ⅲ) ……(12分)
……(12分)
假设存在正整数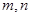 ,且
,且 ,使得
,使得 成等比数列
成等比数列
则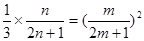 ,所以
,所以
由 得
得 且
且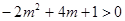
即 ,所以
,所以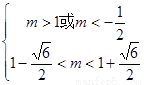
因为 为正整数,所以
为正整数,所以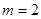 ,此时
,此时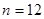
所以满足题意的正整数存在, .…………(15分)
.…………(15分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的前
的前 项和是
项和是 ,满足
,满足 .
. 及前
及前 数列
数列 满足
满足 ,求数列
,求数列 的前
的前 ;
; ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围. 的前
的前 项和为
项和为 ,且满足
,且满足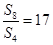 ,则公比
,则公比 =(
)
=(
) B.
B.  C. 2
D.
C. 2
D. 
 的前
的前 项和
项和 ,则
,则 }的前
}的前 项和为
项和为 ,且
,且 ,则数列
,则数列 的公比
的公比 的值为( )
的值为( )