题目内容
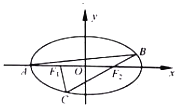
【题目】如图，设点
， 
， 
分别为椭圆
的左顶点和左，右焦点，过点
作斜率为
的直线交椭圆于另一点
，连接
并延长交椭圆于点
.
（1）求点
的坐标（用
表示）；
（2）若
，求
的值.
【答案】（1）
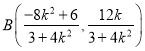（2）
【解析】试题分析：（1）首先求出左顶点
，然后求出直线
方程为： 
，联立椭圆方程与直线方程，消去未知数
，得到关于
的一元二次方程，然后根据韦达定理表示出两根之积，然后就可以得到
点横坐标，再带入直线方程，得出总坐标；（2）易知左焦点
，右焦点
，又根据
，所以
，则
所在直线方程为
，同样可以求出直线
的方程，然后联立两直线方程，可以求出交点
的坐标，将
点坐标带入椭圆方程后，便可以求出
值.
试题解析：（1）设点
，直线
的方程为
，联立
得， 
，
，即
，
，即
.
（2）易知
， 
， 
，
所以直线
， 
方程分别为
， 
，
由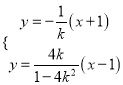
，解得
，代入
，
得
，即
，得
，
所以
.
练习册系列答案
口算能手系列答案
相关题目
