题目内容
已知圆 ,椭圆
,椭圆 ,若
,若 的离心率为
的离心率为 ,如果
,如果 相交于
相交于 两点,且线段
两点,且线段 恰为圆
恰为圆 的直径,求直线
的直径,求直线 与椭圆
与椭圆 的方程。
的方程。
 ,椭圆
,椭圆 ,若
,若 的离心率为
的离心率为 ,如果
,如果 相交于
相交于 两点,且线段
两点,且线段 恰为圆
恰为圆 的直径,求直线
的直径,求直线 与椭圆
与椭圆 的方程。
的方程。直线方程为 ,椭圆方程为:
,椭圆方程为:
 ,椭圆方程为:
,椭圆方程为:
试题分析:由
 ,得
,得 ,
,于是椭圆
 的方程可化为
的方程可化为 ,
,因为线段
 恰为圆
恰为圆 的直径,所以
的直径,所以 过圆心,且圆心为
过圆心,且圆心为 的中点,
的中点,所以可设直线
 的方程为
的方程为 ,
,由
 得:
得: ①
①设
 ,则
,则 ,即
,即 ,得
,得 ,
,因此直线
 的方程为:
的方程为: ,即.
,即.此时,①式即为
 ,
,那么

 ,解得
,解得 ,
,所以椭圆方程为

故所求的直线方程为
 ,椭圆方程为:
,椭圆方程为: .
.点评:解析几何的本质问题是用代数方法解决几何问题,所以一定要注意函数与方程思想、数形结合思想、转化与划归思想等数学思想的应用.

练习册系列答案
相关题目
 与抛物线
与抛物线 的一个交点为M,
的一个交点为M, 为抛物线的焦点,若
为抛物线的焦点,若 ,则b的值为
,则b的值为 

 为椭圆
为椭圆 的左右焦点,P是椭圆上一点,且P到椭圆左准线的距离为
的左右焦点,P是椭圆上一点,且P到椭圆左准线的距离为 为线段
为线段 的中点,则
的中点,则 ( )
( ) 内有一动点
内有一动点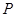 ,已知
,已知 ,且满足
,且满足 ,求
,求 ,过点
,过点 作抛物线
作抛物线 的切线,其切点分别为
的切线,其切点分别为 (其中
(其中 )。
)。 的值;
的值; 相切,求圆的面积。
相切,求圆的面积。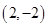 且与双曲线
且与双曲线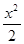 -y
-y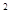 =1有公共渐近线的双曲线方程是( )
=1有公共渐近线的双曲线方程是( )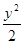 -
-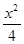 =1
=1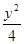 =1
=1 ,
, 为抛物线上一点,
为抛物线上一点, 为
为 关于
关于 轴对称的点,
轴对称的点, 为坐标原点.(1)若
为坐标原点.(1)若 ,求
,求 交抛物线
交抛物线 于
于 两点, 且斜率分别为
两点, 且斜率分别为 ,且
,且 ,求证:直线
,求证:直线 过定点,并求出该定点坐标.
过定点,并求出该定点坐标. 、
、 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 为直线
为直线 上一点,
上一点, 是底角为
是底角为 的等腰三角形,则
的等腰三角形,则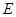 的离心率为( )
的离心率为( )



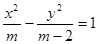 的左焦点与抛物线
的左焦点与抛物线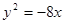 的焦点重合,则
的焦点重合,则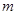 的值为
的值为