题目内容
已知函数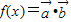 ,其中
,其中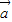 =
=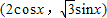 ,
,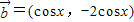 .
.(1)求函数f(x)在区间
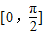 上的单调递增区间和值域;
上的单调递增区间和值域;(2)在△ABC中,a、b、c分别是角A、B、C 的对边,f(A)=-1,且b=1△ABC的面积
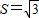 ,求边a的值.
,求边a的值.
【答案】分析:(1)利用向量的数量积,二倍角公式两角差的余弦函数化简函数的表达式,然后结合余弦函数的单调增区间求函数的单调递增区间,确定函数 在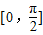 上的单调增区间,单调减区间,然后求出函数的最大值最小值,即可确定函数的值域.
上的单调增区间,单调减区间,然后求出函数的最大值最小值,即可确定函数的值域.
(2))由于f(A)=-1,求得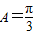 又
又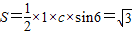 求得c=4最后由余弦定理得a值即可.
求得c=4最后由余弦定理得a值即可.
解答:解:(1)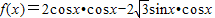 =
=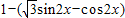 =
=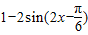 (2分)
(2分)
由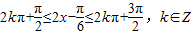 得
得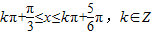 ,
,
又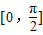 ∴单调增区间为
∴单调增区间为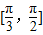 .(4分)
.(4分)
由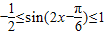 ∴-1≤f(x)≤2∴f(x)∈[-1,2](6分)
∴-1≤f(x)≤2∴f(x)∈[-1,2](6分)
(2)∵f(A)=-1,∴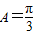 ,(8分)
,(8分)
又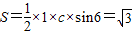 ,∴c=4(10分)
,∴c=4(10分)
由余弦定理得a2=b2+c2-2bccosA=13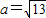 (12分)
(12分)
点评:本题是基础题,考查向量数量积的应用,三角函数的化简求值,单调区间的求法,最值的求法,考查计算能力,注意函数值域的确定中,区间的讨论,单调性的应用是解题的易错点.
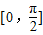 上的单调增区间,单调减区间,然后求出函数的最大值最小值,即可确定函数的值域.
上的单调增区间,单调减区间,然后求出函数的最大值最小值,即可确定函数的值域.(2))由于f(A)=-1,求得
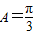 又
又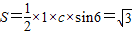 求得c=4最后由余弦定理得a值即可.
求得c=4最后由余弦定理得a值即可.解答:解:(1)
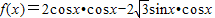 =
=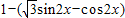 =
=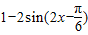 (2分)
(2分)由
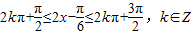 得
得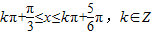 ,
,又
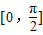 ∴单调增区间为
∴单调增区间为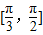 .(4分)
.(4分)由
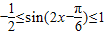 ∴-1≤f(x)≤2∴f(x)∈[-1,2](6分)
∴-1≤f(x)≤2∴f(x)∈[-1,2](6分)(2)∵f(A)=-1,∴
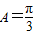 ,(8分)
,(8分)又
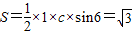 ,∴c=4(10分)
,∴c=4(10分)由余弦定理得a2=b2+c2-2bccosA=13
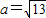 (12分)
(12分)点评:本题是基础题,考查向量数量积的应用,三角函数的化简求值,单调区间的求法,最值的求法,考查计算能力,注意函数值域的确定中,区间的讨论,单调性的应用是解题的易错点.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目






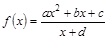 (其中
(其中 是实数常数,
是实数常数, )
) ,函数
,函数 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求 的值;
的值; ,总有
,总有 ,求
,求 的取值范围;
的取值范围; ,
, ,且对任意
,且对任意 时,不等式
时,不等式 恒成立,求负实数
恒成立,求负实数 的取值范围.
的取值范围.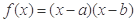 (其中
(其中 )的图象如图(上)所示,则函数
)的图象如图(上)所示,则函数 的图象是( )
的图象是( ) 
