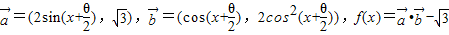题目内容
已知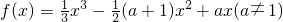
(1)求f(x)的单调区间;
(2)若y=f(x)的图象与x轴有三个交点,求实数a的取值范围.
解:(1)f′(x)=x2-(a+1)x+a=(x-1)(x-a),
当a>1时,由f′(x)>0得x<1或x>a,
∴x∈(-∞,1)和(a,+∞)时,f(x)单调递增,x∈(1,a)时,f(x)单调递减;
当a<1时,由f′(x)>0,得x<a或x>1,
∴x∈(-∞,a)和(1,+∞)时,f(x)单调递增,x∈(a,1)时,f(x)单调递减.
(2)由(1)知x=1和x=a是f(x)得极值点,
a>1时,f(1)是极大值,f(a)是极小值;a<1时,f(a)是极大值,f(1)是极小值,
又y=f(x)的图象与x轴有三个交点,
∴f(1)•f(a)<0,即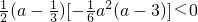 ,
,
∴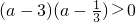 ,
,
∴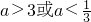 .
.
分析:(1)求出f(x)的导函数,由a大于1和a小于1分两种情况考虑分别令导函数的值大于0,求出x的范围即为函数的递增区间;导函数值小于0时,求出x的范围即为函数的递减区间;
(2)由(1)的导函数值为0时x的值为函数f(x)的极值点,故分a大于1和a小于1时两种情况分别求出f(x)的极大值和极小值,又f(x)函数图象与x轴有三个交点,即极大值与极小值的乘积小于0,列出关于a的不等式,求出不等式的解集即可得到a的取值范围.
点评:此题考查了利用导数研究函数的单调性,以及利用导数研究函数的极值.导函数的值与函数单调性的关系为:令导函数的值大于0,求出x的取值范围即为函数的递增区间;令导函数的值小于0,求出x的取值范围即为函数的递减区间.
当a>1时,由f′(x)>0得x<1或x>a,
∴x∈(-∞,1)和(a,+∞)时,f(x)单调递增,x∈(1,a)时,f(x)单调递减;
当a<1时,由f′(x)>0,得x<a或x>1,
∴x∈(-∞,a)和(1,+∞)时,f(x)单调递增,x∈(a,1)时,f(x)单调递减.
(2)由(1)知x=1和x=a是f(x)得极值点,
a>1时,f(1)是极大值,f(a)是极小值;a<1时,f(a)是极大值,f(1)是极小值,
又y=f(x)的图象与x轴有三个交点,
∴f(1)•f(a)<0,即
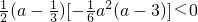 ,
,∴
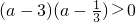 ,
,∴
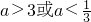 .
.分析:(1)求出f(x)的导函数,由a大于1和a小于1分两种情况考虑分别令导函数的值大于0,求出x的范围即为函数的递增区间;导函数值小于0时,求出x的范围即为函数的递减区间;
(2)由(1)的导函数值为0时x的值为函数f(x)的极值点,故分a大于1和a小于1时两种情况分别求出f(x)的极大值和极小值,又f(x)函数图象与x轴有三个交点,即极大值与极小值的乘积小于0,列出关于a的不等式,求出不等式的解集即可得到a的取值范围.
点评:此题考查了利用导数研究函数的单调性,以及利用导数研究函数的极值.导函数的值与函数单调性的关系为:令导函数的值大于0,求出x的取值范围即为函数的递增区间;令导函数的值小于0,求出x的取值范围即为函数的递减区间.

练习册系列答案
相关题目
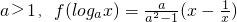



 时,f(x)的最小值为2,求f(x)≥2成立的x的取值集合.
时,f(x)的最小值为2,求f(x)≥2成立的x的取值集合. 的值.
的值.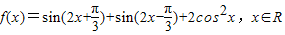
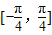 上没有零点,求m的取值范围.
上没有零点,求m的取值范围.