题目内容
已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系中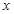
轴的正半轴重合，且两坐标系有相同的长度单位，圆C的参数方程为
（
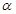为参数），点Q的极坐标为
。
（1）化圆C的参数方程为极坐标方程；
（2）直线
过点Q且与圆C交于M，N两点，求当弦MN的长度为最小时，直线的直角坐标方程。
（1）
（2）
解析试题分析：(1) 先化参数方程为普通方程，然后利用平面直角坐标与极坐标互化公式：
即可；（2）先把Q点坐标化为平面直角坐标，根据圆的相关知识明确：当直线⊥CQ时，MN的长度最小，然后利用斜率公式求出MN斜率.
试题解析：(Ⅰ)圆C的直角坐标方程为
， 2分
又 4分
∴圆C的极坐标方程为 5分
（2）因为点Q的极坐标为，所以点Q的直角坐标为（2，-2） 7分
则点Q在圆C内，所以当直线⊥CQ时，MN的长度最小
又圆心C（1，-1），∴
，
直线的斜率
9分
∴直线的方程为
，即 10分
考点：（1）参数方程与普通方程；（2）平面直角坐标与极坐标；（3）圆的性质.
练习册系列答案
阅读快车系列答案
相关题目
中，直线
的参数方程是
（t是参数）， 以原点为极点，x轴的正半轴为极轴建立极坐标系，若圆C的极坐标方程是ρ＝4cosθ，且直线
.
的参数方程为
为参数)，以坐标原点为极点，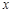
轴的正半轴为极轴建立极坐标系，圆
的极坐标方程为
．
的直角坐标方程；
是直线
≤
的公共点，求
的取值范围．
,以极点为原点,极轴所在直线为x轴建立平面直角坐标系.
)=1,M,N分别为C与x轴,y轴的交点.
中，已知圆
的参数方程
（
为参数），以
为极点，
轴的非负半轴为极轴建立极坐标系.
，射线
与圆
，与直线
的交点为
，求线段
的长.