题目内容

椭圆 x2 + 4y2 = 8 中, AB是长为的动弦 .O为坐标原点 . 求AOB面积的取值范围 .

解析：令 A, B 的坐标为 ( x1 , y1 ) ,( x 2 , y 2 ) , 直线 AB 的方程为 y = kx + b , 代入椭圆方程整理得:  (4k2 +1)x2 + 8kbx + 4(b2－2) = 0 . 故 x1 + x2 =－, x1x2 =.    ( 5 分 )

由  = AB2 = (k2+1)(x2－x1)2 = (k2+1)((x1+x 2)2－4 x1x2) =(2(4k2+1)－b2) 得到

           b2 = 2 (4k2+1)－                                          ( 5 分) 

原点O 到 AB 的距离为 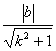, AOB 的面积 S = 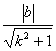, 记 u = , 则有

       S 2= －(u 2－u ) = 4－(u－)2                               ( 5 分)

       u = 4－ 的范围为  , (u = 4 为竖直弦 ). 故 u = 时, max S 2 = 4 , 而 u = 1

时, min S 2 =, 因此 S 的 取值范围是 .                      ( 5 分)

练习册系列答案
相关题目

椭圆x2＋2y2＝1中斜率为2的平行弦的中点的轨迹方程是

[　　]

A．x＋4y＝0(|x|≤1，|y|≤)

B．x＋2y＝0(|x|≤1，|y|≤)

C．x－4y＝0，(|x|≤1，|y|≤)

D．x－2y＝0(|x|≤1，|y|≤)

已知椭圆C的中心在坐标原点，焦点在x轴上，离心率为，它的一个顶点恰好是抛物线x2＝4y的焦点．

(1)求椭圆C的标准方程；

(2)过椭圆C的右焦点作直线l交椭圆C于A、B两点，交y轴于M点，若＝λ1，＝λ2，求λ1＋λ2的值．

设椭圆C1：(a＞b＞0)的一个顶点与抛物线C2：x2＝4y的焦点重合，F1，F2分别是椭圆的左、右焦点，离心率，过椭圆右焦点F2的直线l与椭圆C交于M，N两点．

(Ⅰ)求椭圆C的方程；

(Ⅱ)是否存在直线l，使得·＝－2，若存在，求出直线l的方程；若不存在，说明理由；

(Ⅲ)若AB是椭圆C经过原点O的弦，MN∥AB，求证：为定值．

设椭圆C1：(a＞b＞0)的一个顶点与抛物线C2：x2＝4y的焦点重合，F1、F2分别是椭圆的左、右焦点，离心率，过椭圆右焦点F2的直线l与椭圆C交于M、N两点．

(Ⅰ)求椭圆C的方程；

(Ⅱ)是否存在直线l，使得·＝－1，若存在，求出直线l的方程；若不存在，说明理由．

已知F1、F2分别为椭圆C1：的上、下焦点，其中F1也是抛物线C2：x2＝4y的焦点，点M是C1与C2在第二象限的交点，且|MF1|＝．

(Ⅰ)求椭圆的方程；

(Ⅱ)已知点P(1，3)和圆O：x2＋y2＝b2，过点P的动直线l与圆O相交于不同的两点A，B，在线段AB取一点Q，满足：＝－λ，＝λ(λ≠0且λ≠±1)．求证：点Q总在某定直线上．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网