题目内容
(本小题满分12分)
设点M、N分别是不等边△ABC的重心与外心,已知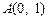 、
、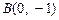 ,且
,且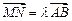 .
.
(1)求动点C的轨迹E;
(2)若直线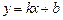 与曲线E交于不同的两点P、Q,且满足
与曲线E交于不同的两点P、Q,且满足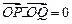 ,求实数
,求实数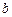 的取值范围。
的取值范围。
设点M、N分别是不等边△ABC的重心与外心,已知
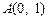 、
、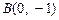 ,且
,且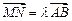 .
.(1)求动点C的轨迹E;
(2)若直线
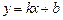 与曲线E交于不同的两点P、Q,且满足
与曲线E交于不同的两点P、Q,且满足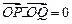 ,求实数
,求实数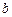 的取值范围。
的取值范围。解:(1)设点 ,则△ABC的重心
,则△ABC的重心 ,∵△ABC是不等边三角形,∴
,∵△ABC是不等边三角形,∴
再设△ABC的外心 . ∵已知
. ∵已知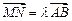 ,∴MN∥AB,∴
,∴MN∥AB,∴ . …………2分
. …………2分
∵点N是△ABC的外心,∴ ,即
,即
化简整理得轨迹E的方程是 …………4分
…………4分
∴动点C的轨迹E是指焦点在轴上的标准位置的一个椭圆(去掉其顶点) …………5分
(2)(理科)将直线方程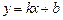 代入轨迹E的方程
代入轨迹E的方程 ,并化简,
,并化简,
得 …………6分
…………6分
依题意,知 ,
, ,且
,且 ,
,
化简,得 ,
, ,且
,且 …………7分
…………7分
设 、
、 ,∵
,∵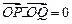 ,∴
,∴ ,即
,即
 …………8分
…………8分
又∵ ,
, ,∴
,∴ ,
,
化简得 …………10分
…………10分
∴ ,
, ,
, ,
, ,
,
解得实数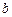 的取值范围是
的取值范围是 或
或 且
且 . …………12分
. …………12分
 ,则△ABC的重心
,则△ABC的重心 ,∵△ABC是不等边三角形,∴
,∵△ABC是不等边三角形,∴
再设△ABC的外心
 . ∵已知
. ∵已知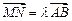 ,∴MN∥AB,∴
,∴MN∥AB,∴ . …………2分
. …………2分∵点N是△ABC的外心,∴
 ,即
,即
化简整理得轨迹E的方程是
 …………4分
…………4分∴动点C的轨迹E是指焦点在轴上的标准位置的一个椭圆(去掉其顶点) …………5分
(2)(理科)将直线方程
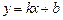 代入轨迹E的方程
代入轨迹E的方程 ,并化简,
,并化简,得
 …………6分
…………6分依题意,知
 ,
, ,且
,且 ,
,化简,得
 ,
, ,且
,且 …………7分
…………7分设
 、
、 ,∵
,∵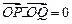 ,∴
,∴ ,即
,即 …………8分
…………8分又∵
 ,
, ,∴
,∴ ,
,化简得
 …………10分
…………10分∴
 ,
, ,
, ,
, ,
,解得实数
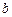 的取值范围是
的取值范围是 或
或 且
且 . …………12分
. …………12分略

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
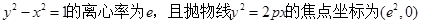 ,则p的值为( )
,则p的值为( ) 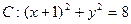 .
. 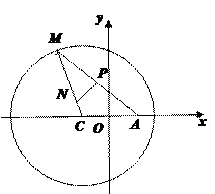
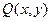 是圆C上一点,求
是圆C上一点,求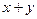 的取值范围;
的取值范围;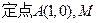 为圆C上一动点,点P在AM上,点N在CM上,且满足
为圆C上一动点,点P在AM上,点N在CM上,且满足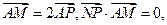 求
求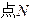 的轨迹的内接矩形的最大面积.
的轨迹的内接矩形的最大面积.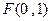 ,一动圆过点
,一动圆过点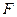 且与圆
且与圆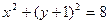 内切,
内切,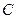 的方程;
的方程;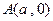 ,点
,点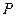 为曲线
为曲线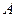 到点
到点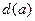 ;
;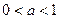 的条件下,设△
的条件下,设△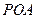 的面积为
的面积为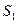 (
(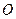 是坐标原点,
是坐标原点,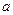 的点),以
的点),以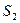 .若正数
.若正数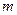 满足
满足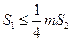 ,问
,问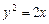 与过焦点的直线交于A、
与过焦点的直线交于A、 B
B 两点,则
两点,则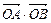 =" " .
=" " .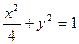 的右焦点,椭圆上的点与点F的最大距离为M,最小距离为N,则椭圆
的右焦点,椭圆上的点与点F的最大距离为M,最小距离为N,则椭圆 的点的坐标是 ( )
的点的坐标是 ( )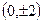
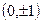
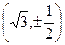
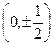
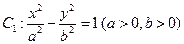 的左、右焦点分别为
的左、右焦点分别为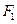 、
、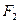 ,抛物线
,抛物线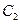 的
的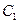 的左准线重合,若双曲线
的左准线重合,若双曲线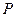 满
满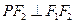 ,则双曲线
,则双曲线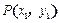 、
、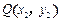 ,定义:
,定义: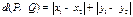 .已知点
.已知点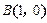 ,点M为直线
,点M为直线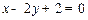 上的动点,则使
上的动点,则使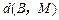 取最小值时点M坐标是.
取最小值时点M坐标是.