Question

叙述并证明余弦定理．

Answer 1

解：余弦定理：三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦之积的两倍．或：在△ABC中，a，b，c为A，B，C的对边，有

a²＝b²＋c²－2bccos A，

b²＝c²＋a²－2cacos B，

c²＝a²＋b²－2abcos C.

证法一：如图，

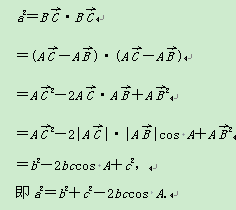
同理可证b²＝c²＋a²－2cacos B，

c²＝a²＋b²－2abcos C.

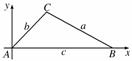
证法二：已知△ABC中A，B，C所对边分别为a，b，c，以A为原点，AB所在直线为x轴建立直角坐标系，则C(bcos A，bsin A)，B(c,0)，

∴a²＝|BC|²＝(bcos A－c)²＋(bsin A)²

＝b²cos²A－2bccos A＋c²＋b²sin²A

＝b²＋c²－2bccos A.

同理可证b²＝c²＋a²－2cacos B，

c²＝a²＋b²－2abcos C.