Question

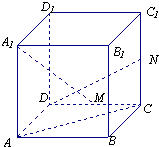如图，在正方体ABCD-A₁B₁C₁D₁中，M，N分别是棱CD，CC₁的中点，则异面直线A₁M与AC所成角的大小是

 

．

Answer 1

分析：通过建立空间直角坐标系，利用两条异面直线的方向向量的夹角即可得出．

解答：解：如图所示，建立空间直角坐标系．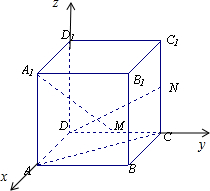
不妨设|AD|=2．则A（2，0，0），C（0，2，0），D（0，0，0），A₁（2，0，2），M（0，1，0）．
∴

AC

=（-2，2，0），

A1M

=（-2，1，-2）．
∴cos＜

AC

，

A1M

＞=

A1M • AC

| A1M | | AC |

=

4+2

4+4 • 4+1+4

=

2

2

．
∴＜

A1M

，

AC

＞=45°．
∴异面直线A₁M与AC所成角的大小是45°．
故答案为45°．

点评：本题考查了通过建立空间直角坐标系利用两条异面直线的方向向量的夹角求出异面直线的夹角的方法，属于基础题．