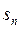题目内容
(本小题满分12分)
在数列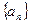 中,
中,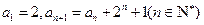 .
.
(Ⅰ)求数列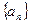 的通项公式
的通项公式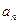 ;(Ⅱ)设数列
;(Ⅱ)设数列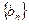 满足
满足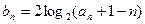 ,证明:
,证明:
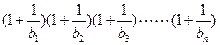
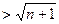 对一切
对一切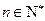 恒成立.
恒成立.
在数列
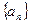 中,
中,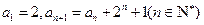 .
.(Ⅰ)求数列
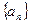 的通项公式
的通项公式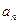 ;(Ⅱ)设数列
;(Ⅱ)设数列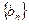 满足
满足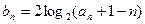 ,证明:
,证明: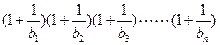
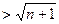 对一切
对一切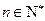 恒成立.
恒成立.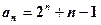
解: ⑴方法一: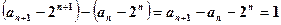 (与
(与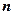 无关)
无关)
故数列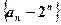 为等差数列,且公差
为等差数列,且公差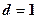 。
。
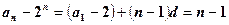 ,
,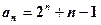 . --------5分
. --------5分
方法二:当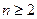 时,由递推关系,
时,由递推关系,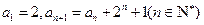 得
得
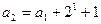 ,
,
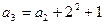
………
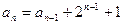 ,将上述n-1个等式相加,得
,将上述n-1个等式相加,得
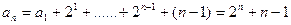
当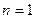 时,亦满足上式.
时,亦满足上式.
综上所述,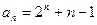
⑵由⑴可知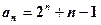 ,∴
,∴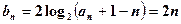 --------6分
--------6分
方法一:数学归纳法
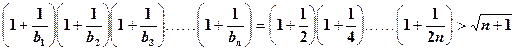
⑴当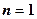 时,
时,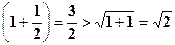 ,不等式成立,
,不等式成立,
⑵假设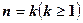 时不等式成立,
时不等式成立,
即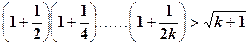 ,
,
那么当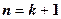 时,
时,
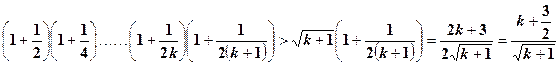
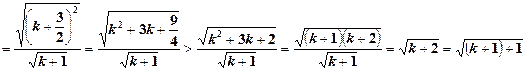
这说明,当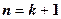 时不等式也成立
时不等式也成立
综上可知,对于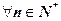 ,原不等式均成立。 ------------12分
,原不等式均成立。 ------------12分
方法二:均值不等式
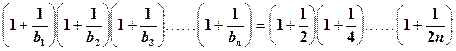
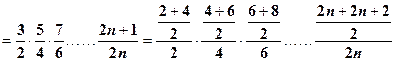
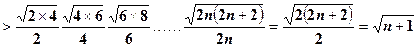 。
。
原不等式得证。 ------------------12分
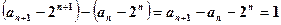 (与
(与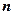 无关)
无关)故数列
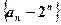 为等差数列,且公差
为等差数列,且公差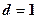 。
。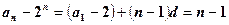 ,
,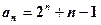 . --------5分
. --------5分方法二:当
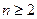 时,由递推关系,
时,由递推关系,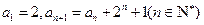 得
得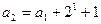 ,
,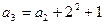
………
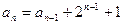 ,将上述n-1个等式相加,得
,将上述n-1个等式相加,得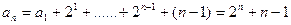
当
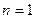 时,亦满足上式.
时,亦满足上式.综上所述,
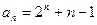
⑵由⑴可知
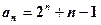 ,∴
,∴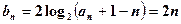 --------6分
--------6分方法一:数学归纳法
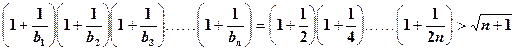
⑴当
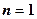 时,
时,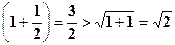 ,不等式成立,
,不等式成立,⑵假设
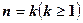 时不等式成立,
时不等式成立,即
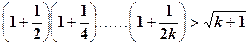 ,
,那么当
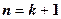 时,
时,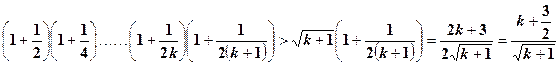
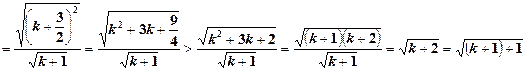
这说明,当
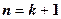 时不等式也成立
时不等式也成立综上可知,对于
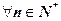 ,原不等式均成立。 ------------12分
,原不等式均成立。 ------------12分方法二:均值不等式
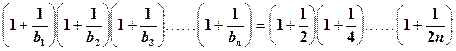
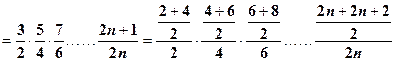
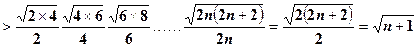 。
。原不等式得证。 ------------------12分

练习册系列答案
相关题目
 }中
}中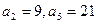 .
.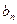 =
=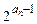 ,求数列
,求数列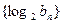 的前
的前 项和
项和 .
.
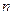 行中从左到右第13与第14个数的比为
行中从左到右第13与第14个数的比为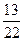 ,求
,求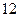 行所有数的和,写出
行所有数的和,写出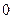 阶)杨辉三角中的所有数的和;
阶)杨辉三角中的所有数的和;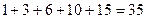 ,事实上,一般地有这样的结论:第
,事实上,一般地有这样的结论:第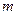 斜列中(从右上到左下)前
斜列中(从右上到左下)前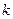 个数之和,一定等于第
个数之和,一定等于第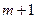 斜列中第
斜列中第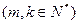 的数学式子表示上述结论,并证明.
的数学式子表示上述结论,并证明.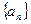 中,
中,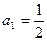 ,点
,点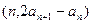 在直线
在直线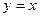 上,其中
上,其中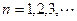
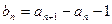 ,求证:数列
,求证:数列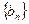 是等比数列;
是等比数列;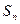 、
、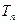 分别为数列
分别为数列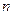 项和,是否存在实数
项和,是否存在实数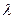 使得数列
使得数列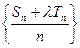 为等差数列?若存在,试求出
为等差数列?若存在,试求出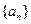 的前
的前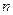 项和为
项和为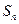 ,且满足
,且满足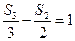 ,则数列
,则数列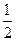
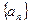 中,
中,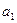 =15,
=15,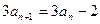 (
(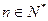 ),则该数列中相邻两项的乘积是负数的是( )
),则该数列中相邻两项的乘积是负数的是( )
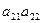
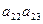
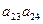
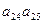
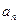 }的前n 项和为
}的前n 项和为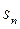 ,已知
,已知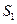 ,
,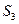 ,
,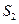 成等差数列
成等差数列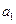 -
-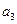 =3,求
=3,求