题目内容
已知双曲线
(a＞0,b＞0)的左、右焦点分别为F1、F2,P为双曲线左支上一点,P到左准线的距离为d且d、|PF1|、|PF2|成等比数列.(1)若y=3x是已知双曲线的一条渐近线,求P点的坐标;
(2)求此双曲线离心率e的取值范围.
解:(1)因双曲线的一条渐近线的方程为y=x,故
,即b=
a.且半焦距c=
=2a,离心率e=2.
设点P的坐标为(x0,y0).
∵d、|PF1|、|PF2|成等比数列,
∴
∴|PF2|=2|PF1|,|PF1|=2d.
又∵|PF2|-|PF1|=2a,故|PF1|=2a,
∴a=d.
∴|x0|=|d+
|=|a+
|=
a.
∵x0＜0,则x0=-
a.
∵P(x0,y0)在双曲线上,∴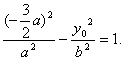
∴y0=±
a.
∴P点的坐标为(-
a,±
a).
(2)由题设知
(e＞1),
∴
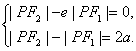
∴|PF1|=
,|PF2|=
.
∵|PF1|+|PF2|≥|F1F2|=2c=2ea,
∵
,又∵a＞0,e＞1,
∴1+e≥e2-e
e2-2e-1≤0.∴1＜e≤1+
.
练习册系列答案
相关题目
(a＞0,b＞0),F1、F2为双曲线的两个焦点，点P在双曲线上，求|PF1|·|PF2|的最小值.
(a＞0,b＞0)的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为
(O为原点),则两条渐近线的夹角为( )
(a>0,b<0)的右焦点为F，若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点，则此双曲线离心率的取值范围是
(a>0,b<0)的右焦点为F，若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点，则此双曲线离心率的取值范围是
(a＞0，b＞0) 的焦点到渐近线的距离是a，则双曲线的离心率的值是 ．