题目内容
已知常数c>0,设命题p:函数y=cx在R上单调递减,命题q:关于x的不等式|x|+|x-2c|>1-c的解集为R.如果命题p∧q为假命题,p∨q为真命题,求常数c的取值范围.
思路解析:本题结合函数的单调性、函数的最值以及命题p∧q、p∨q的真假与p、q的真假间的关系,从而得出结论.
解:函数y=cx在R上单调递减![]() 0<c<1,关于x的不等式|x|+|x-2c|>1-c的解集为R
0<c<1,关于x的不等式|x|+|x-2c|>1-c的解集为R![]() 函数y=x+|x-2c|在R上的函数值恒大于c,而y=x+|x-2c|=
函数y=x+|x-2c|在R上的函数值恒大于c,而y=x+|x-2c|=![]() 故函数y-=x+|x-2c|在R上的最小值为2c,由关于x的不等式|x|+|x-2c|>1-c的解集为R得2c>1-c,c<
故函数y-=x+|x-2c|在R上的最小值为2c,由关于x的不等式|x|+|x-2c|>1-c的解集为R得2c>1-c,c<![]() .
.
要使命题p∧q为假命题,p∨q为真命题,则需命题p、q必为一真一假命题,故
 即
即![]() ≤c<1或
≤c<1或
即c∈![]()
综上,常数c的取值范围为![]() ≤c<1.
≤c<1.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 的定义域为R,命题q:函数
的定义域为R,命题q:函数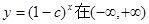 为增函数,若命题p、q有且仅有一个正确,则c的取值范围为
为增函数,若命题p、q有且仅有一个正确,则c的取值范围为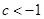 B.
B.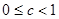 C.
C.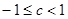 D.
D.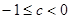
 的定义域为R,命题q:函数
的定义域为R,命题q:函数 为增函数,若命题p、q有且仅有一个正确,则c的取值范围为
为增函数,若命题p、q有且仅有一个正确,则c的取值范围为


