题目内容
设m∈R,函数f(x)=
x3-mx在x=1处取得极值.求:
(Ⅰ)m的值;
(Ⅱ)函数y=f(x)在区间[-3,
]上的最大值和最小值.
| 1 |
| 3 |
(Ⅰ)m的值;
(Ⅱ)函数y=f(x)在区间[-3,
| 3 |
| 2 |
(1)由于函数f(x)=
x3-mx,则f′(x)=x2-m
由f′(1)=0,即x2-m=0
解得m=1,经检验,m=1符合题意
所以m=1
(2)由(1)得f′(x)=x2-1,
列表
且f(-1)=
,f(1)=-
,f(-3)=-7,f(
)=-
,
所以当x∈[-3,
]时,f(x)max=f(-1)=
,f(x)min=f(-3)=-7
| 1 |
| 3 |
由f′(1)=0,即x2-m=0
解得m=1,经检验,m=1符合题意
所以m=1
(2)由(1)得f′(x)=x2-1,
列表
| x | [-3,-1) | -1 | (-1,1) | 1 | (1,
| ||
| f′(x) | + | 0 | - | 0 | + | ||
| f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 8 |
所以当x∈[-3,
| 3 |
| 2 |
| 2 |
| 3 |

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 x3-mx在x=1处取得极值.求:
x3-mx在x=1处取得极值.求: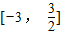 上的最大值和最小值.
上的最大值和最小值.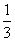 x3-mx在x=1处取得极值,求:
x3-mx在x=1处取得极值,求: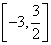 上的最大值和最小值。
上的最大值和最小值。