题目内容
设m∈R，函数f（x）=
x3-mx在x=1处取得极值．求：（Ⅰ）m的值；
（Ⅱ）函数y=f（x）在区间
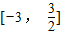上的最大值和最小值．
【答案】分析：（1）根据所给的函数的解析式，对函数求导，f′（1）=0，得到关于m的关系式，解出即可；
（2）对函数求导，写出函数的导函数等于0的x的值，列表表示出在各个区间上的导函数和函数的情况，求出极值，把极值同端点处的值进行比较得到结果．
解答：解：（1）由于函数f（x）=
x3-mx，则f′（x）=x2-m
由f′（1）=0，即x2-m=0
解得m=1，经检验，m=1符合题意
所以m=1
（2）由（1）得f′（x）=x2-1，
列表
且f（-1）=
，f（1）=
，f（-3）=-7，f（
）=
，
所以当x∈[-3，
]时，f（x）max=f（-1）=
，f（x）min=f（-3）=-7
点评：本题考查函数的最值问题，解题的关键是写出函数的极值和函数在两个端点处的值，把这些值进行比较，得到最大值和最小值．
（2）对函数求导，写出函数的导函数等于0的x的值，列表表示出在各个区间上的导函数和函数的情况，求出极值，把极值同端点处的值进行比较得到结果．
解答：解：（1）由于函数f（x）=
x3-mx，则f′（x）=x2-m 由f′（1）=0，即x2-m=0
解得m=1，经检验，m=1符合题意
所以m=1
（2）由（1）得f′（x）=x2-1，
列表
| x | [-3，-1） | -1 | （-1，1） | 1 | （1， |
| f′（x） | + | - | + | ||
| f（x） | 递增 | 极大值 | 递减 | 极小值 | 递增 |
，f（1）=，f（-3）=-7，f（）=，所以当x∈[-3，
]时，f（x）max=f（-1）=，f（x）min=f（-3）=-7点评：本题考查函数的最值问题，解题的关键是写出函数的极值和函数在两个端点处的值，把这些值进行比较，得到最大值和最小值．
练习册系列答案
相关题目
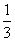x3-mx在x=1处取得极值，求：
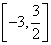上的最大值和最小值。