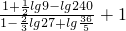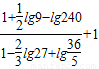题目内容
（1）化简：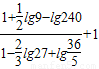
（2）已知：lg（x-1）+lg（x-2）=lg2，求x的值．
【答案】分析：（1）直接利用对数的运算性质化简要求的式子，从而得到结果．
（2）由题意可得 lg（x-1）（x-2）=lg2，故有 x-2=1，或 x-2=-2 （舍去），由此解得 x的值．
解答：解：（1）
=
+1=
+1=
=
=0．
（2）∵lg（x-1）+lg（x-2）=lg2，∴lg（x-1）（x-2）=lg2，故有 x-2=1，或 x-2=-2 （舍去），解得 x=3．
点评：本题主要考查对数的运算性质的应用，注意对数函数的定义域，属于基础题．
（2）由题意可得 lg（x-1）（x-2）=lg2，故有 x-2=1，或 x-2=-2 （舍去），由此解得 x的值．
解答：解：（1）
=+1=+1===0．（2）∵lg（x-1）+lg（x-2）=lg2，∴lg（x-1）（x-2）=lg2，故有 x-2=1，或 x-2=-2 （舍去），解得 x=3．
点评：本题主要考查对数的运算性质的应用，注意对数函数的定义域，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，求
