题目内容
已知正方形ABCD—A1B1C1D1的棱长为a,P在AB上,且PB=2PA.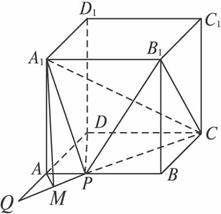
(1)求二面角A1PCA的余弦值;
(2)求B1到面A1PC的距离.
答案:解法一:(1)如下图,延长CP与DA交于Q点,过A作AM⊥PQ,M为垂足,连结A1M,
则A1M⊥PQ,∴∠A1MA为二面角A1-PC-A的平面角.

依题意知:AP=![]() a,BP=
a,BP=![]() a,∴AQ=
a,∴AQ=![]() BC=
BC=![]() a,
a,
Rt△APQ斜边PQ上的高AM=![]() ,
,
Rt△A1AM中,tan∠A1MA=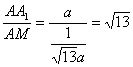 ,∴cos∠A1MA=
,∴cos∠A1MA=![]() .
.
(2)设B1到面A1PC的距离为h,则由:![]() .
.
可得![]()
![]() ·h=
·h=![]() ·BC,
·BC,
易知:BC=a,![]() ,在Rt△PBC中,易求得PC=
,在Rt△PBC中,易求得PC=![]() ,
,
又由(1)知,A1M=![]() ,
,
∴![]() PC·A1M=
PC·A1M=![]() ,
,
因此,![]() a2·h=
a2·h=![]() a2·a,∴h=
a2·a,∴h=![]() a.
a.
解法二:以D为坐标原点建立如下图所示的空间直角坐标系.

则A(a,0,0),B(a,a,0),C(0,a,0),D(0,0,0).
A1(a,0,a),B1(a,a,a),C1(0,a,a),D1(0,0,a).
由PB=2PA知P(a,![]() a,0).
a,0).
(1)![]() =(0,
=(0,![]() a,-a),
a,-a),![]() =(-a,
=(-a,![]() a,0).设平面A1PC的法向量为n1=(x,y,z),
a,0).设平面A1PC的法向量为n1=(x,y,z),
则由![]() ·n1=
·n1=![]() ay-az=0.
ay-az=0.![]() ·n1=-ax+
·n1=-ax+![]() ay=0.
ay=0.
设:x=![]() y,z=
y,z=![]() y,
y,
取y=3,得n1=(2,3,1).
设n2为平面ABCD的法向量,易知n2=(0,0,1).
则cos〈n1,n2〉=![]() ,
,
∴二面角A1PCA的余弦值为![]() .
.
(2)由(1)知平面A1PC的法向量n1=(2,3,1),又A1B1=(0,a,0),
∴B1到平面A1PC的距离d=|A1B1|·|cos〈n1,![]() 〉|=|
〉|=|![]() |·
|·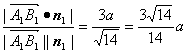 .
.

| AB |
| BC |
| AC |
| A、0 | ||
| B、2 | ||
C、
| ||
D、2
|
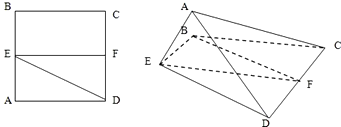 已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为θ(0<θ<π).
已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为θ(0<θ<π). (2008•虹口区二模)(理)已知正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,
(2008•虹口区二模)(理)已知正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,