题目内容
3. 如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口E是AB的中点,F,G分别落在AD,BC上,且AB=20m,AD=10$\sqrt{3}$m,设∠GEB=θ.
如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口E是AB的中点,F,G分别落在AD,BC上,且AB=20m,AD=10$\sqrt{3}$m,设∠GEB=θ.(1)试将污水管道的长度l表示成θ的函数,并写出定义域;
(2)当管道长度l为何值时,污水净化效果最好,并求此时管道的长度.
分析 (1)根据题意分别表示出EG,EF,FG,进而表示出l的表达式.
(2)设sinθ+cosθ把l转化为关于t的方程,利用单调性确定最大值.
解答 (1)因为EG=$\frac{10}{cosθ}$,EF=$\frac{10}{sinθ}$,FG=$\frac{10}{sinθcosθ}$,
l=10($\frac{1}{sinθ}$+$\frac{1}{cosθ}$+$\frac{1}{sinθcosθ}$),θ∈[$\frac{π}{6}$,$\frac{π}{3}$].
(2)l=$\frac{1+sinθ+cosθ}{sinθcosθ}$•10
设t=sinθ+cosθ=$\sqrt{2}$sin(θ+$\frac{π}{4}$)∈[$\frac{\sqrt{3}+1}{2}$,$\sqrt{2}$],
l=$\frac{2(t+1)}{{t}^{2}-1}$•10=$\frac{20}{t-1}$,为减函数,
∴当θ=$\frac{π}{6}$或$\frac{π}{3}$时,有最大值20($\sqrt{3}$+1),
答:当θ=$\frac{π}{6}$或$\frac{π}{3}$时,污水净化效果最好,l最大值20($\sqrt{3}$+1)m.
点评 本题主要考查了三角形问题的实际应用.解题的重要的地方是建立数学模型,把实际问题转化为数学问题来解决.

练习册系列答案
相关题目
14.已知命题p:?x∈R,x2-2x-4≤0,则¬p为( )
| A. | ?x∈R,x2-2x-4≥0 | B. | ?x0∈R,x02-2x0-4>0 | ||
| C. | ?x∉R,x2-2x+4≤0 | D. | ?x0∈R,x02-2x0-4>0 |
 定义运算“?”,两个实数a,b的“a?b”运算如图所示,若输入a=2cos$\frac{2015π}{3}$b=2,则输出P的值为( )
定义运算“?”,两个实数a,b的“a?b”运算如图所示,若输入a=2cos$\frac{2015π}{3}$b=2,则输出P的值为( )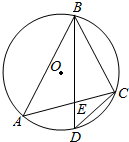 如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于E.
如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于E.