Question

过点A（-2，4）引倾斜角为135°的直线l交抛物线y²=2px(p＞0)于P₁、P₂两点，若|AP₁|、|P₁P₂|、|AP₂|成等比数列，求P的值.

Answer 1

解：设l的参数方程为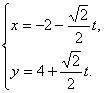代入抛物线方程整理得t²+(p)t+32+8p=0.

∴|AP₁|·|AP₂|=|t₁·t₂|=32+8p.

又|P₁P₂|²=(t₁+t₂)²-4t₁t₂=8p²+32p,

∴8p²+32p=32+8p，即p²+3p-4=0.

∴p=1.