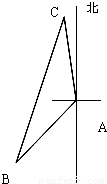
题目内容
我舰在敌岛A南偏西50°相距12海里的B处,发现敌舰正由岛沿北偏西10°的方向以10海里/时的速度航行.问我舰需以多大速度,沿什么方向航行才能用2小时追上敌舰?
思路分析:先根据方位角画出图,根据题意及所画出的方位图可知本题实际上可归纳为已知三角形的两边和它们的夹角,求第三边及角,即△ABC中,已知AB=12,AC=10×2=20,∠CAB=180°-(10°+50°)=120°,求BC及∠ABC.
由BC长进而可求出我舰航行速度,由∠ABC的大小进而可求出我舰航行方向.
解:如图,在△ABC中,

∵AB=12,AC=20,∠CAB=120°,
由余弦定理得
BC2=AC2+AB2-2·AB·AC·cos∠BAC
=202+122-2×20×12×cos120°
=400+144+240
=784.
∴BC=28.
∴我舰的追击速度是![]() ,即14海里/时.
,即14海里/时.
在△ABC中,由正弦定理,得![]() =
=![]() ,
,
即sinB=![]() =
= =
=![]() .
.
∴∠ABC≈38.2°,50°-38.2°=11.8°.
故我舰航行的方向约为北偏东11.8°.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
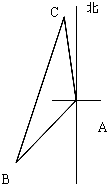 如图所示,我舰在敌岛A南偏西50° 且与A相距6海里的B处,发现敌舰正由岛A沿北偏西10°的方向以5海里/小时的速度航行,我舰要用2小时在C处追上敌舰,问需要的速度是多少?
如图所示,我舰在敌岛A南偏西50° 且与A相距6海里的B处,发现敌舰正由岛A沿北偏西10°的方向以5海里/小时的速度航行,我舰要用2小时在C处追上敌舰,问需要的速度是多少?