题目内容
 如图,已知PA⊥正方形ABCD所在平面,E、F分别是AB,PC的中点,∠PDA=45°.(1)求证:EF∥面PAD.
如图,已知PA⊥正方形ABCD所在平面,E、F分别是AB,PC的中点,∠PDA=45°.(1)求证:EF∥面PAD.(2)求证:面PCE⊥面PCD.
分析:(1)取PD中点为G,证明EFGA为平行四边形,由EF∥AG,证明EF∥面PAD.
(2)由线面垂直的判定定理证明AG⊥面PCD,从而得到EF⊥面PCD,面PCE⊥面PCD.
(2)由线面垂直的判定定理证明AG⊥面PCD,从而得到EF⊥面PCD,面PCE⊥面PCD.
解答:解:(1)取PD中点为G,连FG、AG,∵F,G分别为中点,∴FG∥CD,且 FG=
CD.AE∥CD,且 AE=
CD,
即四边形EFGA为平行四边形,∴EF∥AG,又EF?面PAD,AG?面PAD,∴EF∥面PAD.
(2)PA⊥面ABCD∴PA⊥AD,PA⊥CD∴Rt△PAD中,∠PDA=45°∴PA=AD,AG⊥PD,又CD⊥AD,CD⊥PA,
且PA∩AD=A,∴CD⊥面PAD,∴CD⊥AG,又PD∩CD=D,∴AG⊥面PCD,
由(1)知EF∥AG∴EF⊥面PCD,又EF?面PCE,∴面PCE⊥面PCD.
| 1 |
| 2 |
| 1 |
| 2 |
即四边形EFGA为平行四边形,∴EF∥AG,又EF?面PAD,AG?面PAD,∴EF∥面PAD.
(2)PA⊥面ABCD∴PA⊥AD,PA⊥CD∴Rt△PAD中,∠PDA=45°∴PA=AD,AG⊥PD,又CD⊥AD,CD⊥PA,
且PA∩AD=A,∴CD⊥面PAD,∴CD⊥AG,又PD∩CD=D,∴AG⊥面PCD,
由(1)知EF∥AG∴EF⊥面PCD,又EF?面PCE,∴面PCE⊥面PCD.
点评:本题考查两个平面垂直的判定定理的应用以及证明线面平行的方法.

练习册系列答案
相关题目
 如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.
如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.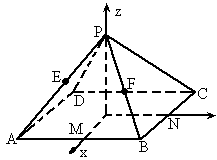
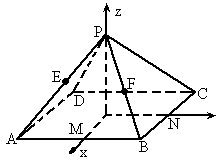
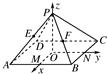 如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.
如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.