题目内容

四棱锥S-ABCD中，已知
AC
=（1，1，1），
AD
=（10，-5，5），
AB
=（-1，2，0），
SA
=（2，1，-3）．
（1）求证：BC∥AD；
（2）四边形ABCD的面积；
（3）求四棱锥S-ABCD的体积，并说明理由．
分析：（1）由空间向量的坐标运算得出
BC
、
AD
的坐标，从而得到
AD
=5
BC
，可得
AD
∥
BC
，即BC∥AD；
（2）利用向量的夹角公式算出cos∠BAD=-
4
30
，从而sin∠BAD=
1-cos2∠BAD
=
14
30
，算出点B到AD的距离d=|
AB
|sin∠BAD=
21
3
，再利用梯形的面积公式即可算出四边形ABCD的面积；
（3）经计算得
SA
•
AD
=0且
SA
•
AB
=0，可得
SA
⊥
AD
且
SA
⊥
AB
，得SA⊥平面ABCD，SA即为四棱锥S-ABCD的高，算出|
AD
|=
14
，利用锥体的体积公式即可算出四棱锥S-ABCD的体积．
解答：解：（1）∵
AC
=（1，1，1），
AB
=（-1，2，0），
∴
BC
=
AC
-
AB
=（2，-1，1），
∵
AD
=（10，-5，5），∴
AD
=5（2，-1，1）=5
BC

可得
AD
∥
BC
，即BC∥AD；
（2）∵
AB
=（-1，2，0），
AD
=（10，-5，5），
∴cos∠BAD=
-1×10+2×(-5)+0×5
5
•5
6
=-
4
30

可得sin∠BAD=
1-cos2∠BAD
=
14
30
，
∴点B到AD的距离d=|
AB
|sin∠BAD=
5
×
14
30
=
21
3

∵BC∥AD，且BC≠AD，|
BC
|=
6
且|
AD
|=5
6

∴梯形ABCD的面积为SABCD=
1
2
（|
BC
|+|
AD
|）×
21
3
=3
14
；
（3）∵
AD
=（10，-5，5），
AB
=（-1，2，0），
SA
=（2，1，-3）．
∴
SA
•
AD
=2×10+1×（-5）+（-3）×5=0，且
SA
•
AB
=2×（-1）+1×2+（-3）×0=0
由此可得
SA
⊥
AD
，
SA
⊥
AB
，得SA⊥平面ABCD
∵|
AD
|=
22+12+(-3)2
=
14

∴四棱锥S-ABCD的体积V=
1
3
SABCD×|
AD
|=
1
3
×3
14
×
14
=14．
点评：本题给出几个空间向量的坐标，求由它们构成的四棱锥的体积．着重考查了空间向量的坐标运算、向量的夹角公式、模的公式和面积、体积公式等知识，属于中档题．
练习册系列答案
相关题目
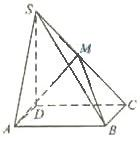精英家教网如图，四棱锥S-ABCD中，底面ABCD为矩形，SD⊥底面ABCD，AD=
2
，DC=SD=2，点M在侧棱SC上，∠ABM=60°
（I）证明：M是侧棱SC的中点；
（2）求二面角S-AM-B的大小．
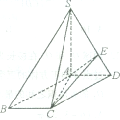精英家教网如图，在四棱锥S-ABCD中，底面ABCD为平行四边形，SA⊥平面ABCD，AB=2，AD=1，SB=
7
，∠BAD=120°，E在棱SD上，且SE=3ED．
（I）求证：SD⊥平面AEC；
（II）求直线AD与平面SCD所成角的大小．
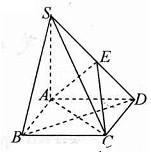精英家教网如图，在底面是菱形的四棱锥S-ABCD中，SA=AB=2，SB=SD=2
2
．
（1）证明：BD⊥平面SAC；
（2）问：侧棱SD上是否存在点E，使得SB∥平面ACE？请证明你的结论．
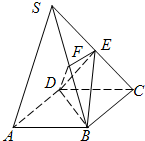如图，在四棱锥S-ABCD中，底面ABCD为正方形，侧棱SD⊥底面ABCD，SD=AD，DF⊥SB垂足为F，E是SD的中点．
（Ⅰ）证明：SA∥平面BDE；
（Ⅱ）证明：平面SBD⊥平面DEF．
如图，四棱锥S-ABCD中．ABCD为矩形，SD⊥AD，且SD⊥AB，AD=a（a＞0），AB=2AD，SD=
3
AD．E为CD上一点，且CE=3DE．
（1）求证：AE⊥平面SBD；
（2）M、N分别在线段CD、SB上的点，是否存在M、N，使MN⊥CD且MN⊥SB，若存在，确定M、N的位置；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网