题目内容
已知F1(-
,0),F2(
,0)为平面内的两个定点,动点P满足|PF1|+|PF2|=4,记点P的轨迹为曲线г.
(Ⅰ)求曲线г的方程;
(Ⅱ)判断原点O关于直线x+y-1=0的对称点R是否在曲线г包围的范围内?说明理由.
(说明:点在曲线г包围的范围内是指点在曲线г上或点在曲线г包围的封闭图形的内部.)
(Ⅲ)设Q是曲线г上的一点,过点Q的直线l 交 x 轴于点F(-1,0),交 y 轴于点M,若|
|=2|
|,求直线l 的斜率.
| 2 |
| 2 |
(Ⅰ)求曲线г的方程;
(Ⅱ)判断原点O关于直线x+y-1=0的对称点R是否在曲线г包围的范围内?说明理由.
(说明:点在曲线г包围的范围内是指点在曲线г上或点在曲线г包围的封闭图形的内部.)
(Ⅲ)设Q是曲线г上的一点,过点Q的直线l 交 x 轴于点F(-1,0),交 y 轴于点M,若|
| MQ |
| QF |
(Ⅰ)由题意可知,点P到两定点F1(-
,0),F2(
,0)的距离之和为定值4,
所以点P的轨迹是以F1(-
,0),F2(
,0)为焦点的椭圆.
又a=2,c=
,所以b=
.
故所求方程为
+
=1.
(Ⅱ)解法一:设原点O关于直线x+y-1=0的对称点为R(m,n),
由点关于直线的对称点的性质得:
,解得
即R(1,1).
此时
+
=
<1,∴R在曲线г包围的范围内.
解法二:设原点O关于直线x+y-1=0的对称点为R(m,n),
由点关于直线的对称点的性质得:
,解得
即R(1,1),
∴直线OR的方程:y=x
设直线OR交椭圆
+
=1于G和H,
由
得:
或
即G(
,
),H(-
,-
).
显然点R在线段GH上.∴点R在曲线г包围的范围内.
(Ⅲ)由题意知直线l 的斜率存在,设直线l 的斜率为k,直线l 的方程为y=k(x+1).
则有M(0,k),设Q(x1,y1),由于Q,F,M三点共线,且|
|=2|
|,
根据题意,得(x1,y1-k)=±2(x1+1,y1),解得
或
.
又点Q在椭圆上,所以
+
=1或
+
=1.
解得k=0,k=±4.
综上,直线l 的斜率为k=0,k=±4.
| 2 |
| 2 |
所以点P的轨迹是以F1(-
| 2 |
| 2 |
又a=2,c=
| 2 |
| 2 |
故所求方程为
| x2 |
| 4 |
| y2 |
| 2 |
(Ⅱ)解法一:设原点O关于直线x+y-1=0的对称点为R(m,n),
由点关于直线的对称点的性质得:
|
|
此时
| 12 |
| 4 |
| 12 |
| 2 |
| 3 |
| 4 |
解法二:设原点O关于直线x+y-1=0的对称点为R(m,n),
由点关于直线的对称点的性质得:
|
|
∴直线OR的方程:y=x
设直线OR交椭圆
| x2 |
| 4 |
| y2 |
| 2 |
由
|
|
|
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
显然点R在线段GH上.∴点R在曲线г包围的范围内.
(Ⅲ)由题意知直线l 的斜率存在,设直线l 的斜率为k,直线l 的方程为y=k(x+1).
则有M(0,k),设Q(x1,y1),由于Q,F,M三点共线,且|
| MQ |
| QF |
根据题意,得(x1,y1-k)=±2(x1+1,y1),解得
|
|
又点Q在椭圆上,所以
| (-2)2 |
| 4 |
| (-k)2 |
| 2 |
(-
| ||
| 4 |
(
| ||
| 2 |
解得k=0,k=±4.
综上,直线l 的斜率为k=0,k=±4.

练习册系列答案
相关题目
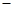 2,0),F2(2,0),点P满足|PF1|-|PF2|=2,记点P的轨迹为S,过点F2作直线
2,0),F2(2,0),点P满足|PF1|-|PF2|=2,记点P的轨迹为S,过点F2作直线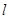 与轨迹S交于P、Q两点,过P、Q作直线x=的垂线PA、QB,垂足分别为A、B,记λ=|AP|·|BQ|.
与轨迹S交于P、Q两点,过P、Q作直线x=的垂线PA、QB,垂足分别为A、B,记λ=|AP|·|BQ|.