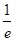题目内容
经过原点且与曲线y＝
相切的方程是( )
相切的方程是( )A．x＋y＝0或 ＋y＝0 | B．x－y＝0或＋y＝0 |
| C．x＋y＝0或－y＝0 | D．x－y＝0或－y＝0 |
A
设切点(x0，y0)，则切线的斜率为k＝
，另一方面，y′＝()′＝
，故y′(x0)＝k，即
＝＝
⇒x02＋18x0＋45＝0，得x0(1)＝－3，x0(2)＝－15，对应有y0(1)＝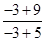
＝3，y0(2)＝
＝
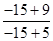，因此得两个切点A(－3,3)或B(－15，)，从而得y′A＝－1，y′B＝－
．由于切线过原点，故得切线lA：y＝－x或lB：y＝－．
，另一方面，y′＝()′＝，故y′(x0)＝k，即＝＝⇒x02＋18x0＋45＝0，得x0(1)＝－3，x0(2)＝－15，对应有y0(1)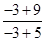＝＝3，y0(2)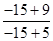＝＝，因此得两个切点A(－3,3)或B(－15，)，从而得y′A＝－1，y′B＝－．由于切线过原点，故得切线lA：y＝－x或lB：y＝－．
练习册系列答案
阅读快车系列答案
相关题目
，曲线
在点
处的切线方程为
为函数
与
图象的公共点，以
与两曲线都相切，则实数
的最大值为 ．
，和抛物线相切且与直线
平行的的直线方程为 （ ）
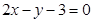
－x2＋1(0<x<2)的图象上任意点处切线的倾斜角记为α，则α的最小值是( )
在点（1,1）处的切线方程 。
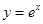在点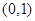
处的切线斜率为（ ）
