题目内容
(12分)设函数 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为
(I)求
(II)证明:
 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为
(I)求

(II)证明:

(I)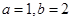 ;(II)详见解析.
;(II)详见解析.
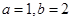 ;(II)详见解析.
;(II)详见解析.试题分析:(I)由切点
 在切线
在切线 上,代入得
上,代入得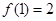 ①.由导数的几何意义得
①.由导数的几何意义得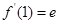 ②,联立①②求
②,联立①②求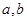 ;(II)证明
;(II)证明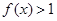 成立,可转化为求函数
成立,可转化为求函数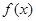 的最小值,只要最小值大于1即可.该题不易求函数
的最小值,只要最小值大于1即可.该题不易求函数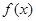 的最小值,故可考虑将不等式结构变形为
的最小值,故可考虑将不等式结构变形为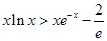 ,分别求函数
,分别求函数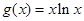 和
和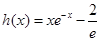 的最值,发现
的最值,发现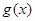 在
在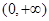 的最小值为
的最小值为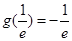 ,
,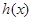 在
在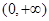 的最大值为
的最大值为 .且不同时取最值,故
.且不同时取最值,故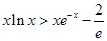 成立,即
成立,即 注意该种方法有局限性
注意该种方法有局限性 只是不等式
只是不等式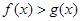 的充分不必要条件,意即当
的充分不必要条件,意即当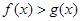 成立,最值之间不一定有上述关系.
成立,最值之间不一定有上述关系.试题解析:(I)函数的定义域为
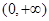 .
.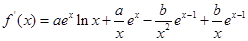 .
.由题意可得,
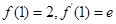 .故
.故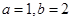 .
.(II)由(I)知,
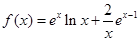 ,从而
,从而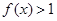 等价于
等价于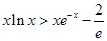 ,设函数
,设函数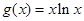 ,则
,则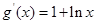 .所以当
.所以当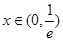 时,
时,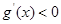 ;当
;当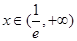 时,
时,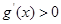 .故
.故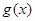 在
在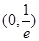 递减,在
递减,在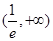 递增,从而
递增,从而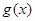 在
在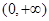 的最小值为
的最小值为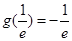 .设
.设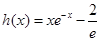 ,则
,则 .所以当
.所以当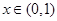 时,
时,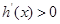 ;当
;当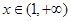 时,
时,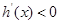 .故
.故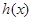 在
在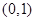 递增,在
递增,在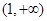 递减,从而
递减,从而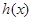 在
在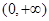 的最大值为
的最大值为 .综上,当
.综上,当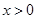 时,
时,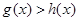 ,即
,即 .
.【考点定位】1、导数的几何意义;2、利用导数判断函数的单调性;3、利用导数求函数的最值.

练习册系列答案
相关题目
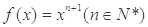 的图象与直线
的图象与直线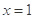 交于点P,若图象在点P处的切线与x轴交点的横坐标为
交于点P,若图象在点P处的切线与x轴交点的横坐标为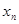 ,则
,则 +
+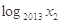 +…+
+…+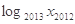 的值为( )
的值为( )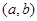 上的可导函数
上的可导函数 的导函数
的导函数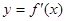 的图象如右所示,则
的图象如右所示,则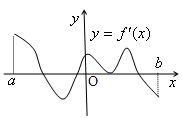
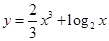 ;
;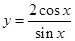 .
. .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 的取值范围;
的取值范围; ,若在
,若在 上至少存在一点
上至少存在一点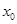 ,使得
,使得 >
> 成立,求实数
成立,求实数 相切的方程是( )
相切的方程是( ) +y=0
+y=0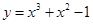 在点
在点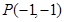 处的切线方程是 ;
处的切线方程是 ; ,在
,在 处连续,则实数
处连续,则实数 的值为 .
的值为 .