Question

隔河测算A，B两目标的距离，在岸边取C，D两点，测得CD=200m，∠ADC=105°，∠BDC=15°，∠BCD=120°，∠ACD=30°，则A，B间的距离　　m．

Answer 1

考点：

余弦定理；正弦定理．

专题：

计算题；解三角形．

分析：

依题意，利用正弦定理可求得AD，BD，再利用余弦定理即可求得AB．

解答：

解：作图如下：

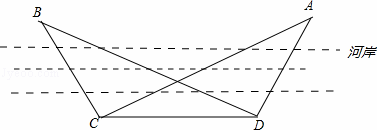
∵CD=200m，∠ADC=105°，∠ACD=30°，∠BDC=15°，∠BCD=120°，

∴∠CAD=∠CBD=45°，∠BDA=90°；

∴在△ACD中，由正弦定理=，即=，

∴AD=100；

在△BCD中，同理可求BD=100．

在直角三角形BDA中，由勾股定理得AB===．

故A，B间的距离为200m．

故答案为200．

点评：

本题考查正弦定理与余弦定理，求得AD，BD是关键，考查作图与运算能力，属于中档题．