题目内容
在整数集 中,被
中,被 除所得余数为
除所得余数为 的所有整数组成一个“类”,记为
的所有整数组成一个“类”,记为 ,即
,即 ,
, .给出如下四个结论:
.给出如下四个结论:
① ;
;
② ;
;
③ ;
;
④当且仅当“ ”整数
”整数 属于同一“类”.
属于同一“类”.
其中,正确结论的个数为.
A. | B. | C. | D. |
C
解析试题分析:①∵2011÷5=402…1,∴2011∈[1],故①对;
②∵-3=5×(-1)+2,∴对-3∉[3];故②错;
③∵整数集中的数被5除的数可以且只可以分成五类,故Z=[0]∪[1]∪[2]∪[3]∪[4],故③对;
④∵整数a,b属于同一“类”,∴整数a,b被5除的余数相同,从而a-b被5除的余数为0,反之也成立,故“整数a,b属于同一“类”的充要条件是“a-b∈[0]”.故④对.
∴正确结论的个数是3.故选C..
考点:新定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
| |||||||||||||||
设 是集合
是集合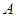 到集合
到集合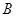 的映射,若
的映射,若 ,则
,则 为( )
为( )
A. | B. | C. | D. |
已知集合 ,若对于任意
,若对于任意 ,存在
,存在 ,使得
,使得 成立,则称集合M是“垂直对点集”.给出下列四个集合:
成立,则称集合M是“垂直对点集”.给出下列四个集合:
① ; ②
; ② ;
;
则以下选项正确的是()
| A.①是“垂直对点集” ,②不是“垂直对点集” |
| B.①不是“垂直对点集”,②是“垂直对点集” |
| C.①②都是“垂直对点集” |
| D.①②都不是“垂直对点集” |
在映射 ,
, ,且
,且 ,则A中的元素
,则A中的元素 对应集合B中的元素为( )
对应集合B中的元素为( )
A. | B. | C. | D. |
满足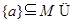
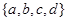 的集合
的集合 共有( )
共有( )
| A.6个 | B.5个 | C.8个 | D.7个 |
若集合A={0,1},B={-1,a2},则“a=1”是“A∩B={1}”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知集合A={x∈R||x|≥2},B={x∈R|x2-x-2<0},且R为实数集,则下列结论正确的是( )
| A.A∪B=R | B.A∩B≠∅ |
| C.A⊆(∁RB) | D.A?(∁RB) |
若集合A={x∈R|ax2+ax+1=0}中只有一个元素,则a等于( ).
| A.4 | B.2 | C.0 | D.0或4 |
 ,则f(x)的“姊妹点对”有( )个.
,则f(x)的“姊妹点对”有( )个.