题目内容
设对于任意的实数x,y,函数f(x,)g(x)满足f(x+1)=
f(x),且f(0)=2,g(x+y)=g(x)+2y,g(3)=5,an=f(n),bn=g(n),n?N*. (Ⅰ)求数列an,bn的通项公式bn的通项公式
(Ⅱ)设cn=anbn,求数列cn的n和Sn的前n和Sn
| 1 | 2 |
(Ⅱ)设cn=anbn,求数列cn的n和Sn的前n和Sn
分析:(Ⅰ)要求{an},{bn}的通项,从f(x+1)=
f(x)中构造an+1与an的关系,bn的通项公式,从f(x+1)=
f(x)中构造an+1与an的关系
=
,从g(x+y)-g(x)=2y,构造bn+1-bn=2,分别利用等差数列及等比数列的通项公式求an,bn;
(Ⅱ)cn=anbn是等差数列与等比数列的积,用乘公比错位相减求和.
| 1 |
| 2 |
| 1 |
| 2 |
| an+1 |
| an |
| 1 |
| 2 |
(Ⅱ)cn=anbn是等差数列与等比数列的积,用乘公比错位相减求和.
解答:解:(Ⅰ)∵f(x+1)=
f(x),f(0)=2
∴f(1)=
f(0)=1,
∵an=f(n),an+1=f(n+1),a1=f(1)=
f(0)=1
=
=
所以{an},以
为公比,以1为首项的等比数列
∴an=(
)n-1
∵g(x+y)=g(x)+2y,∴g(x+1)-g(x)=2
bn=g(n),∴bn+1-bn=g(n+1)-g(n)=2
Sn=1•(
)0+2•(
)1+2•(
)n-1-(2n-1)(
)n)
∵b3=g(3)=5,∴b1=1
数列{bn}以1为首项,以2为公差的等差数列
bn=1+(n-1)×2=2n-1
(Ⅱ)cn=anbn=(2n-1)•(
)n-1
Sn=c1+c2+…+cn
=1•(
)0+3•(
)1+ …+(2n-1)(
)n-1
sn=1•(
)1+3•(
)2+…+(2n-1)(
)n
∴Sn=6-
| 1 |
| 2 |
∴f(1)=
| 1 |
| 2 |
∵an=f(n),an+1=f(n+1),a1=f(1)=
| 1 |
| 2 |
| an+1 |
| an |
| f(n+1) |
| f(n) |
| 1 |
| 2 |
所以{an},以
| 1 |
| 2 |
∴an=(
| 1 |
| 2 |
∵g(x+y)=g(x)+2y,∴g(x+1)-g(x)=2
bn=g(n),∴bn+1-bn=g(n+1)-g(n)=2
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵b3=g(3)=5,∴b1=1
数列{bn}以1为首项,以2为公差的等差数列
bn=1+(n-1)×2=2n-1
(Ⅱ)cn=anbn=(2n-1)•(
| 1 |
| 2 |
Sn=c1+c2+…+cn
=1•(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴Sn=6-
| 3+2n |
| 2n-1 |
点评:本题主要考查等差、等比数列递推关系的基本方法,同时考查构造法及推理论证的能力,而乘公比错位相减求和是数列求和的一个难点与易错点.

练习册系列答案
相关题目
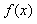 ,
,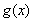 满足
满足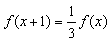 , 且f(0)=3,g(x+y)=g(x)+
, 且f(0)=3,g(x+y)=g(x)+ 和
和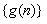 的通项公式;
的通项公式;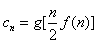 ,求数列
,求数列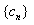 的前n项和Sn;
的前n项和Sn; 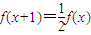 ,且f(0)=2,g(x+y)=g(x)+2y,g(3)=5,an=f(n),bn=g(n),n?N*. (Ⅰ)求数列an,bn的通项公式bn的通项公式
,且f(0)=2,g(x+y)=g(x)+2y,g(3)=5,an=f(n),bn=g(n),n?N*. (Ⅰ)求数列an,bn的通项公式bn的通项公式