题目内容
11. 已知四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形且AA1⊥底面ABCD,AA1=4,E为BC的中点,F为CC1的中点.
已知四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形且AA1⊥底面ABCD,AA1=4,E为BC的中点,F为CC1的中点.(1)求证:直线EF∥平面ABD1;
(2)求三棱锥F-A1EC1的体积.
分析 (1)证明EF∥AD1,利用线面平行的判定定理,即可证明直线EF∥平面ABD1;
(2)三棱锥F-A1EC1的体积=三棱锥A1-FEC1的体积,求三棱锥F-A1EC1的体积.
解答 (1)证明:连接BC1,则BC1∥AD1,
∵E为BC的中点,F为CC1的中点.
∴EF∥BC1,
∴EF∥AD1,
∵EF?平面ABD1,AD1?平面ABD1,
∴直线EF∥平面ABD1;
(2)解:∵AA1⊥底面ABCD,∴AA1⊥AB,
∵AD⊥AB,AD∩AA1=A,
∴AB⊥平面AD1,
∵AA1=4,AB=2
∴三棱锥F-A1EC1的体积=三棱锥A1-FEC1的体积=$\frac{1}{3}×\frac{1}{2}×\frac{1}{2}×1×2$=$\frac{1}{6}$.
点评 本题考查线面平行的判定定理,考查三棱锥F-A1EC1的体积,正确运用线面平行的判定定理是关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
2.在△ABC中,角A,B,C的对边分别为a,b,c,函数f(x)=(a+b+c)x2+2$\sqrt{ab}$x+a+b-c恰有一个零点,则角C的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
6.f(x)=x3+ax2+bx+c在区间(1,2)上有三个零点,则( )
| A. | f(1)f(2)≤$\frac{1}{64}$ | B. | f(1)f(2)<$\frac{1}{64}$ | C. | f(1)f(2)>-$\frac{1}{64}$ | D. | f(1)f(2)≥-$\frac{1}{64}$ |
3.函数f(x)=log2(1-3x)的定义域是( )
| A. | (0,+∞) | B. | [0,+∞) | C. | (-∞,0) | D. | (-∞,0] |
 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=∠BCD=90°,面PAD⊥面ABCD,PA=PD=CD=BC=1,AB=2,AD=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=∠BCD=90°,面PAD⊥面ABCD,PA=PD=CD=BC=1,AB=2,AD=$\sqrt{2}$.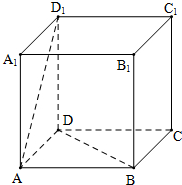 如图,正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是线段AD1和BD上的点,且D1P:PA=DQ:QB=5:12.
如图,正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是线段AD1和BD上的点,且D1P:PA=DQ:QB=5:12.