题目内容
【题目】直四棱柱ABCD﹣A1B1C1D1中，底面ABCD为菱形，且∠BAD=60°，A1A=AB，E为BB1延长线上的一点，D1E⊥面D1AC．设AB=2．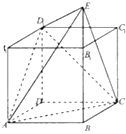 
（1）求二面角E﹣AC﹣D1的大小；
（2）在D1E上是否存在一点P，使A1P∥面EAC？若存在，求D1P：PE的值；不存在，说明理由．
【答案】
（1）解：设AC与BD交于O，
如图以O为原点，OA，OB，为x轴，y轴，过O作面ABCD的垂线为z轴，建立空间直角坐标系，
则A（ 
，0，0），B（0，1，0），C（﹣ ，0，0），D（0，﹣1，0），D1（0，﹣1，2），
设E（0，1，2+h），
则 
=（0，2，h）， 
=（2 ，0，0）， 
=（ 
），
∵D1E⊥平面D1AC，∴D1E⊥AC，D1E⊥D1A，
∴2﹣2h=0，∴h=1，即E（0，1，3），
∴ =（0，2，1）， 
=（﹣ ，1，3），
设平面EAC的法向量为 
=（x，y，z），
则由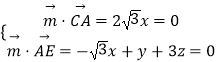 
，令z=﹣1，得 =（0，3，﹣1），
∵D1E⊥面D1AC，∴平面D1AC的法向量为 =（0，2，1），
∴cos＜ 
＞= 
= 
= 
，
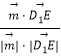∴二面角E﹣AC﹣D1的大小为45°．
（2）解：设 
= 
=λ（ 
），
得 = 
=（0， 
， 
），
∴ 
= 
+ =（﹣ ，﹣1，0）+（0， ， ）=（﹣ ， 
， ），
∵A1P∥面EAC，∴ ⊥ ，
∴﹣ 
=0，
解得 
，
∴存在点P使A1P∥面EAC，此时D1P：PE=2：3．
【解析】（1）设AC与BD交于O，以O为原点，OA，OB，为x轴，y轴，过O作面ABCD的垂线为z轴，建立空间直角坐标系，利用向量法能求出二面角E﹣AC﹣D1的大小．（2）设 = =λ（ ），得 =（0， ， ）， =（﹣ ， ， ），由此能求出存在点P使A1P∥面EAC，此时D1P：PE=2：3．
【考点精析】关于本题考查的直线与平面平行的判定，需要了解平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行才能得出正确答案．
