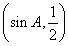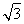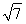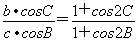题目内容
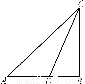
如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.问:点B在什么位置时,四边形OACB面积最大?

即∠AOB=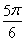 时,四边形OACB面积最大
时,四边形OACB面积最大
【解析】设∠AOB=α,在△AOB中,由余弦定理得AB2=OA2+OB2-2×OA×OBcos∠AOB=12+22-2×1×2×cosα
=5-4cosα,
于是,四边形OACB的面积为
S=S△AOB+S△ABC=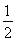 OA·OBsinα+
OA·OBsinα+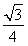 AB2
AB2
=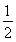 ×2×1×sinα+
×2×1×sinα+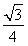 (5-4cosα)
(5-4cosα)
=sinα-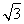 cosα+
cosα+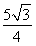 =2sin
=2sin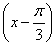 +
+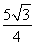 .
.
因为0<α<π,所以当α-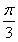 =
=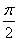 ,α=
,α=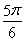 ,即∠AOB=
,即∠AOB=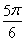 时,
时,
四边形OACB面积最大

练习册系列答案
相关题目