题目内容
12.在平面直角坐标系xoy中,已知直线l:x+y+a=0与点A(0,2),若直线l上存在点M满足|MA|2+|MO|2=10(O为坐标原点),则实数a的取值范围是( )| A. | (-$\sqrt{5}$-1,$\sqrt{5}$-1) | B. | [-$\sqrt{5}$-1,$\sqrt{5}$-1] | C. | (-2$\sqrt{2}$-1,2$\sqrt{2}$-1) | D. | [-2$\sqrt{2}$-1,2$\sqrt{2}$-1] |
分析 设M(x,-x-a),由已知条件利用两点间距离公式得x2+(-x-a)2+x2+(-x-a-2)2=10,由此利用根的判别式能求出实数a的取值范围.
解答 解:设M(x,-x-a),
∵直线l:x+y+a=0,点A(0,2),直线l上存在点M,满足|MA|2+|MO|2=10,
∴x2+(x+a)2+x2+(-x-a-2)2=10,
整理,得4x2+2(2a+2)x+a2+(a+2)2-10=0①,
∵直线l上存在点M,满足|MA|2+|MO|2=10,
∴方程①有解,
∴△=4(2a+2)2-16[a2+(a+2)2-10]≥0,
解得:-2$\sqrt{2}$-1≤a≤2$\sqrt{2}$-1,
故选:D.
点评 本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意两点间距离公式和一元二次方程式根的判别式的合理运用.

练习册系列答案
相关题目
3.在棱长为1的正方体ABCD-A1B1C1D1中,P为B1C1的中点,那么直线CP与B1D1所成角的余弦值是( )
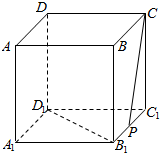

| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
20.函数y=sin(-2x)的单凋减区间是( )
| A. | [$\frac{π}{2}$+2kπ,$\frac{3π}{2}$+2kπ],k∈Z | B. | [$\frac{π}{2}$+2kπ,$\frac{3π}{4}$+2kπ],k∈Z | ||
| C. | [π+2kπ,3π+2kπ],k∈Z | D. | [-$\frac{π}{4}$+kπ,$\frac{π}{4}$+kπ],k∈Z |
4.设数列{an}是单调递增的等差数列,前三项的和为6,a4=8,则它的首项是( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
7.如果一个家庭有两个小孩,则两个孩子是一男一女的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |